SKETCH THE GRAPH OF RATIONAL FUNCTION
The function which is in the form of f(x) / g(x) is rational function. To draw the graph of rational function, we have to discuss the following.
i) Horizontal asymptote :
Horizontal asymptotes are horizontal lines that the graph of the function approaches as x tends to +∞ or −∞.
A horizontal asymptote is a special case of a slant asymptote.
Let
deg N(x) = the degree of a numerator
and
deg D(x) = the degree of a denominator
Case 1 :
Degree of numerator = degree of denominator
y = leading coefficient of N(x)/leading coefficient of D(x).
Case 2 :
Degree of numerator < degree of denominator
y = 0, which is the x – axis.
Case 3 :
degree of numerator > degree of denominator
There is no horizontal asymptote.
ii) Vertical Asymptotes :
The Vertical Asymptotes of a rational function are found using the zeros of the denominator.
iii) Oblique or slant asymptote :
A slant (oblique) asymptote occurs when the polynomial in the numerator is a higher degree than the polynomial in the denominator.
ii) y-intercept :
The point where the curve is intersecting y-axis is known as y-intercept.
iii) Finding some points :
By applying some random values of x, we can find out the values of y.
i) Determine the asymptotes.
ii) Find the coordinates of all points where the function crosses its asymptotes.
iii) Sketch the graph of the function
iv) Discuss the behavior of the function as it approaches its asymptotes.
Problem 1 :
Solution :
Let the function be f(x) / g(x)
i) Horizontal asymptote :
Highest exponent of numerator f(x) = 0
Highest exponent of denominator g(x) = 1
The denominator is having highest exponent. So, the horizontal asymptote is x -axis or y = 0.
ii) Vertical asymptote :
x - 2 = 0
At x = 2
x-intercept :
When y = 0, x + 3 = 0 ==> x = -3
When x = 3, y = 3/2 ==> 1.5
Since the denominator is a quadratic function, one part of the graph will be a parabola.
iii) Sketching the graph :
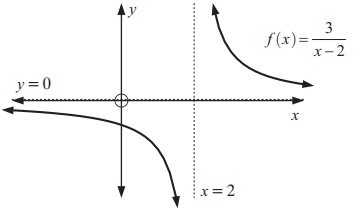
iv) End behavior of function :
|
When x -> 2-, y ->-∞ When x -> 2+, y ->∞ |
When x -> ∞, y -> 0+ When x -> -∞, y -> 0- |
Problem 2 :
Solution :
Let the function be f(x) / g(x)
i) Horizontal asymptote :
Highest exponent of numerator f(x) = 0
Highest exponent of denominator g(x) = 1
The denominator is having highest exponent. So, the horizontal asymptote is x -axis or y = 0.
Vertical asymptote :
x + 1 = 0
At x = -1
ii) When x = -2, y = 5
When x = 0, y = -1
y-intercept, at x = 0
(0, -1)
iii) Sketching the graph :
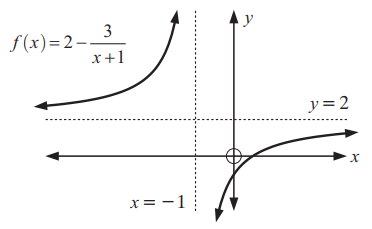
iv) End behavior of the function :
|
When x -> 2-, y ->-∞ When x -> 2+, y ->∞ |
When x -> ∞, y -> 0+ When x -> -∞, y -> 0- |
Problem 3 :
Solution :
Let the function be f(x) / g(x)
i) Horizontal asymptote :
Highest exponent of numerator f(x) = 1
Highest exponent of denominator g(x) = 2
The denominator is having highest exponent. So, the horizontal asymptote is x -axis or y = 0.
ii) Vertical asymptote :
|
x + 1 = 0 x = -1 |
x - 2 = 0 x = 2 |
ii) When x = -2, y = 0.125
y-intercept, at x = 0
(0, -1.5)
iii) Sketching the graph :
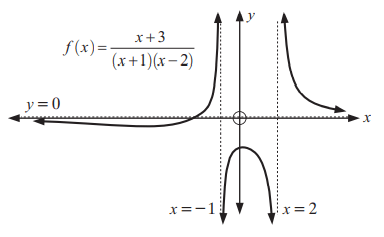
iv) End behavior of the function :
|
When x -> -1-, y ->∞ When x -> -1+, y ->-∞ When x -> 2-, y ->-∞ When x -> 2+, y ->∞ |
When x -> ∞, y -> 0+ When x -> -∞, y -> 0- |
Problem 4 :
Solution :
Let the function be f(x) / g(x)
i) Horizontal asymptote :
y = [x(x - 3) + 2] / (x - 3)
y = (x2 - 3x + 2) / (x - 3)
Highest exponent of numerator f(x) = 2
Highest exponent of denominator g(x) = 1
The numerator is having highest exponent. So, the oblique asymptote is at y = x.
ii) Vertical asymptote :
x - 3 = 0
x = 3
When x = 0, y = -0.6
iii) Sketching the graph :
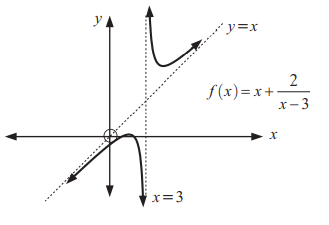
iv) End behavior of the function :
|
When x -> 3-, y ->-∞ When x -> 3+, y ->∞ |
When x -> ∞, y ->x+ When x -> -∞, y ->x- |
Problem 5 :
Solution :
Let the function be f(x) / g(x)
i) Horizontal asymptote :
Highest exponent of numerator f(x) = 2
Highest exponent of denominator g(x) = 2
Equation of horizontal asymptote is y = 1
ii) Vertical asymptote :
When equate the denominator to 0, we get unreal values. So, there is no vertical asymptote.
When x = 0, y = -0.6
iii) Sketching the graph :
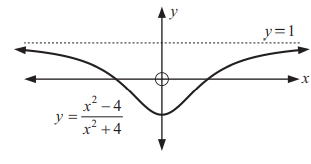
iv) End behavior :
When x -> ∞, y ->1-
When x -> -∞, y ->1-
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling