SIMPLIFY RADICALS BY FINDING PERFECT SQUARE FACTORS

Simplify each expression by factoring to find perfect squares and then taking their root.

Problem 1 :

√75

Solution :

Find the perfect square factor of 75.

= √75

= √(25×3)

= √(5×5×3)

= 5√3

So, the answer is 5√3

Problem 2 :

√16

Solution :

Find the factors of 16.

= √16

= √(4×4)

= 4

So, the answer is 4.

Problem 3 :

√36

Solution :

Find the factors of 36.

= √36

= √(6×6)

= 6

So, the answer is 6.

Problem 4 :

√64

Solution :

Find the factors of 64.

= √(8×8)

= 8

So, the answer is 8.

Problem 5 :

√80

Solution :

Find the perfect square factor of 80.

= √80

= √(16×5)

= √(4×4×5)

= 4√5

So, the answer is 4√5.

Problem 6 :

√30

Solution :

We cannot decompose 30 as a product of perfect square, we decompose 30 as

= √(10×3) (or) √(6×5) (or) √(12×5)

We will not get any product of two same terms, so the result is it cannot be simplified further. 

Note : 

To find the exact value, we can use calculator.

Problem 7 :

√8

Solution :

Find the perfect square factor of 8.

= √8

= √(4 × 2)

= √(2 × 2 × 2)

= 2√2

So, the answer is 2√2.

Problem 8 :

√18

Solution :

Find the perfect square factor of 18.

= √18

= √(9 × 2)

= √(3 × 3 × 2)

= 3√2

So, the answer is 3√2.

Problem 9 :

√32

Solution :

Find the perfect square factor of 32.

= √32

= √(16 × 2)

= √(4 × 4 × 2)

= 4√2

So, the answer is 4√2.

Problem 10 :

√12

Solution :

Find the perfect square factor of 12.

= √12

= √(4 × 3)

= 2√3

So, the answer is 2√3.

Problem 11 :

√108

Solution :

Find the perfect square factor of 108.

= √108

= √(36 × 3)

= √(6 x 3 × 3)

= 6√3

So, the answer is 6√3.

Problem 12 :

√125

Solution :

= √125

= √(25 × 5)

= √(5 x 5 × 5)

= 5√5

So, the answer is 5√5.

Problem 13 :

√50

Solution :

= √50

= √(25 × 2)

= √(5 x 5 × 5)

= 5√2

So, the answer is 5√2.

Problem 14 :

√175

Solution :

= √175

= √(25 × 7)

= √(5 x 5 × 5)

= 5 √7

So, the answer is 5√7.

Problem 15 :

The circumference C of the art room in a mansion is approximated by the formula C ≈ 2π √[a² + b² /2]. Approximate the circumference of the room.

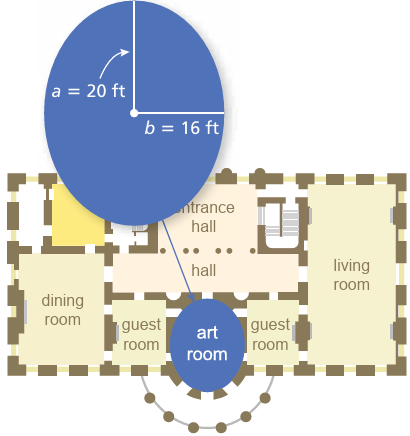
Solution :

C ≈ 2π √[a² + b² /2]

Where a = 20 ft and b = 16 ft

Applying these values, we get

C ≈ 2π √[20² + 16² /2]

≈ 2π √[(400 + 256) /2]

≈ 2π √[656/2]

≈ 2π √328

Decomposing √328, we get

≈ 2π √(2 x 2 x 2 x 41)

≈ 4π √(2 x 41)

≈ 4π √82

Problem 16 :

26 a perfect square?

Solution :

= √26

By decomposing √26, we get

= √(2 x 13)

Since we dont have two same numbers inside the square root, it is not factorable. Then it is not perfect square.

Problem 17 :

Can the square of an integer be a negative number? Explain.

Solution :

By squaring the negative number, we will get positive number as result. Because negative x negative will give positive as result.

Problem 18 :

Does √256 represent the positive square root of 256, the negative square root of 256, or both? Explain.

Solution :

√256 = √(16 x 16)

= ±16

So, for both.

Problem 19 :

The area of the base of a square notepad is 9 square inches. What is the length of one side of the base of the notepad?

Solution :

Area of base of square notepad = 9 square inches

side x side = 9

(side)² = 9

side = √9

side = √(3 x 3)

= 3 inches

So, one side of the base of the notepad is 3 inches.

Problem 20 :

The kinetic energy K (in joules) of a falling apple is represented by K = v²/2 , where v is the speed of the apple (in meters per second). How fast is the apple traveling when the kinetic energy is 32 joules?

Solution :

K = v²/2

Here k = 32 joules

32 = v²/2

32(2) = v²

v² = 64

v = √64

v = √(8 x 8)

v = 8

So, speed of the apple is 8 meters per second.

Problem 21 :

The area of the triangle is represented by the formula A = √s(s − 21)(s − 17)(s − 10) , where s is equal to half the perimeter. What is the height of the triangle?

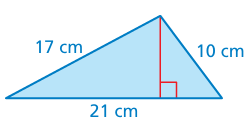
Solution :

Here side lengths are 21 cm, 17 cm and 10 cm

Let a, b and c be the sides of the triangle.

a = 21, b = 17 and c = 10

s = (a + b + c)/2

= (21 + 17 + 10) / 2

= 48/2

= 24

Given that A = √s(s − 21)(s − 17)(s − 10)

Applying the value of s, we get

= √24(24 − 21)(24 − 17)(24 − 10)

= √24 x 3 x 7 x 14

= √2 x 2 x 2 x 3 x 3 x 7 x 2 x 7

= 2 x 2 x 3 x 7

= 84 square cm