SIMILAR AND CONGURENT FIGURES

Congruent Figures

Two figures are congruent if they have the same shape and the same size. If two figures are congruent, then corresponding angles are congruent and corresponding sides are congruent. The triangles at the right are congruent. Matching arcs show congruent angles, and matching tick marks show congruent sides.

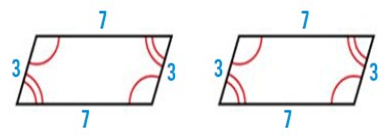
The symbol ≅ is used to say these two shapes congruent.

Similar Figures

Two figures are similar if they have the same shape but not necessarily the same size. If two figures are similar, then corresponding angles are congruent and the ratios of the lengths of corresponding sides are equal.

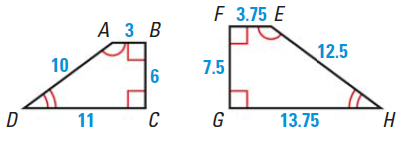
The symbol ~ is used to say the above shapes are similar.

Problem 1 :

Two angles are congruent if they have:

(a) Same name     b) Equal measures

(c) Unequal measures  (d) None of these

Solution :

If two shapes are having same side lengths and angle measures, the shapes are congruent.

So, the answer is equal measures.

Problem 2 :

If a ∆ ABC ≅ ∆ PQR, then AB is equal to:

(a) QR   (b) PQ    (c) PR     (d) None of these

Solution :

Corresponding side of AB is PQ.

Problem 3 :

In ∆ ABC and ∆PQR, AB = 4 cm, BC = 5 cm, AC = 6 cm and PQ = 4 cm, QR = 5 cm, PR = 6 cm, then which of the following is true:

(a) ∆ ABC ≅ ∆ QRP     (b) ∆ ABC ≅ ∆ PQR

(c) ∆ ABC ≅ ∆ PRQ     (d) ∆ ABC ≅ ∆ QPR

Solution :

The corresponding sides of given triangles ABC and PQR are equal.

Corresponding side of AB is PQ,

Corresponding side of BC is QR,

and

Corresponding side of AC is PR

So, ∆ ABC ≅ ∆ PRQ is correct.

Complete the similarity statement for the similar figures and then find the scale factor. Write proportions and solve for missing side lengths.

Problem 4 :

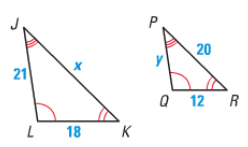
Solution :

∠LJK = ∠QPR

∠JLK = ∠PQR

Since the triangles are equiangular, the above triangles are similar, Comparing the corresponding sides.

JL/PQ = LK/QR/ = JK/PR

21/y = 18/12 = x/20

Problem 5 :

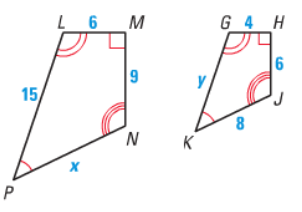
Solution :

∠MLP = ∠HGK

∠LMN = ∠GNJ

Since the shapes are equiangular, the above shapes are similar, Comparing the corresponding sides.

LP/GK = LM/GH = PN/.KJ = MN/HJ

15/y = 6/4 = x/8 = 9/6