SHORTEST DISTANCE FROM THE CENTER OF A CIRCLE TO THE CHORD

Problem 1 :

In figure, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB. What is the length of CD?

a) 2 cm     b) 3 cm     c) 4 cm     d) 5 cm

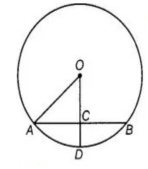
Solution:

OC is perpendicular on chord AB.

OC bisects the chord AB

AC = CB

Now, AC + CB = AB

AC + CB = 8

AC = 8/2

AC = 4 cm

Δ OCA is a right angles triangle.

AO² = AC² + OC²

5² = 4² + OC²

25 = 16 + OC²

OC² = 9

OC = 3

Since, OD is the radius of the circle.

OA = OD = 5 cm

CD = OD - OC

= 5 - 3

= 2 cm

So, option (a) is correct.

Problem 2 :

If AB = 12 cm, BC = 16 cm and AB is perpendicular to  BC, then the radius of the circle passing through the points A, B and C is

a) 6 cm   b) 8 cm    c) 10 cm    d) 12 cm

Solution:

Use Pythagoras theorem in right angled Δ ABC.

AC² = AB² + BC²

AC² = (12)² + (16)²

AC² = 144 + 256

AC² = 400

AC = √400

AC = 20 cm

Radius of circle = 1/2 (AC)

= 1/2 × 20

= 10 cm

Hence, the radius of circle is 10 cm.

So, option (c) is correct.

Problem 3 :

In a circle radius is 13 cm, a chord is drawn at a distance of 12 cm from the centre. Find the length of the chord.

a) 5 cm   b) 10 cm    c) 15 cm    d) 30 cm

Solution:

Given, hypotenuse H = Radius of circle = 13 cm

P = perpendicular distance = 12 cm

L be the length of half chord.

By using Pythagoras Theorem,

H² = L² + P²

L = √(13² - 12²)

L = √(169 - 144)

L = √25

L = 5 cm

Now, length of the chord is 2L = 10 cm.

Therefore the length of chord will be 10 cm.

So, option (b) is correct.

Problem 4 :

Three points A, B and C are located on a circle which are equidistant from one another. If the radius of the circle is 20m the calculate the length of AB.

Solution:

In equilateral triangle,

AD is the median of Δ ABC and it passes through the center O.

O is the centroid of the Δ ABC. OA is the radius of the triangle.

By using Pythagoras Theorem in Δ ABD,

So, the length of AB is 20√3 m.