SEQUENCE OF TRANSFORMATIONS ON FUNCTIONS

Problem 1 :

Describe how each transformation or sequence of transformations of the function

f(x) = 3x²

will affect the number of zeros the function has.

a) a vertical stretch of factor 2

b) a horizontal translation 3 units to the left

c) a horizontal compression of factor 2 and then a reflection in the x-axis

d) a vertical translation 3 units down

e) a horizontal translation 4 units to the right and then a vertical translation 3 units up

f) a reflection in the x-axis, then a horizontal translation 1 unit to the left, and then a vertical translation 5 units up

Solution :

f(x) = 3x²

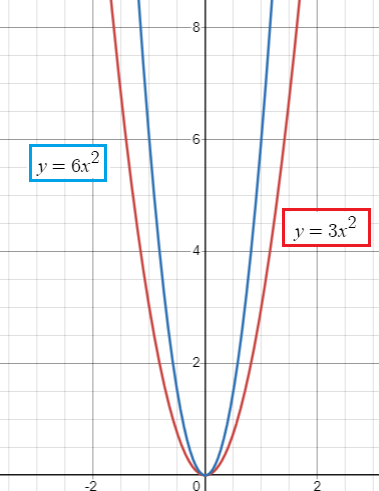
a) a vertical stretch of factor 2

Vertical stretch = 2

f(x) = 2(3x²)

f(x) = 6x²

b) a horizontal translation 3 units to the left

Horizontal translation = 3 units, since it is left, we should apply -3

f(x) = 3(x - h)²

Applying -3 for h, we get

f(x) = 3(x - (-3))²

= 3(x + 3)²

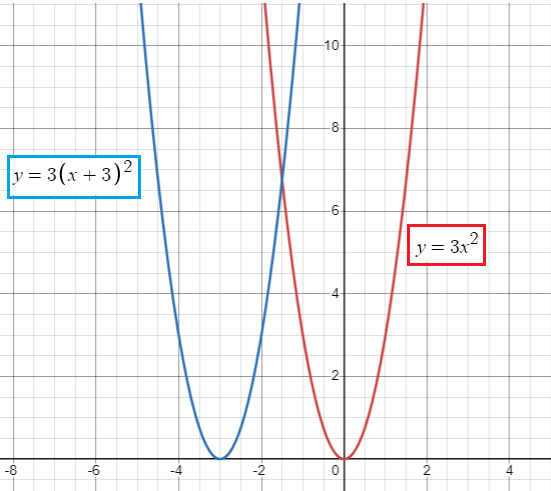
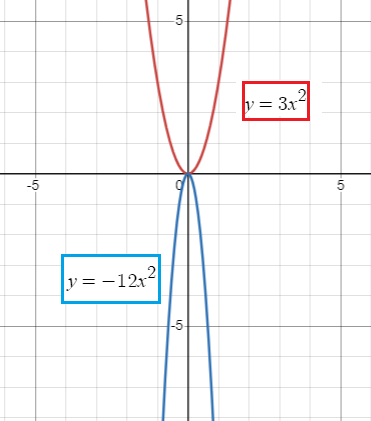
c) a horizontal compression of factor 2 and then a reflection in the x-axis

Horizontal compression, a = 2

reflection across the x-axis, so y = -y

f(x) = 3x²

= -3(2x)²

= -3(4x²)

= -12x²

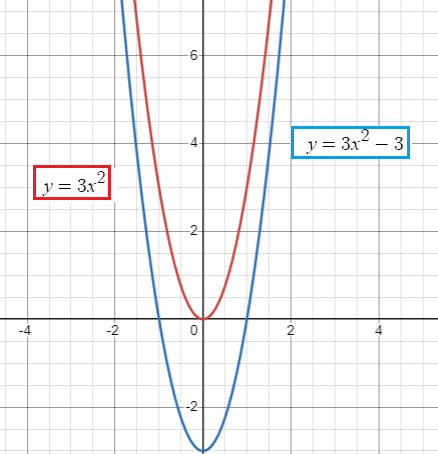
d) a vertical translation 3 units down

Vertical translation, so k = -3 (since it is down 3 units)

f(x) = 3x²

f(x) = 3x² - 3

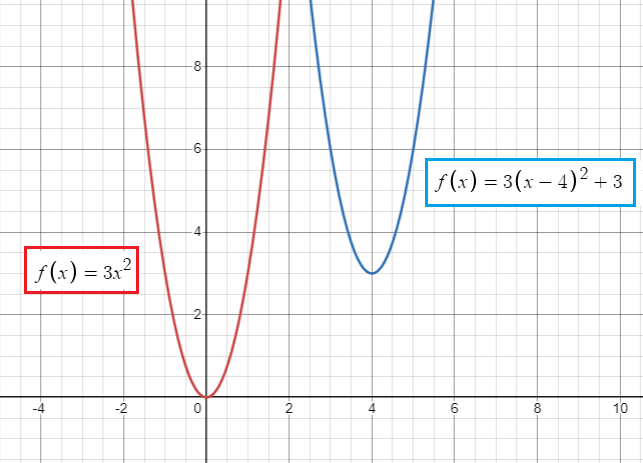
e) a horizontal translation 4 units to the right and then a vertical translation 3 units up

f(x) = 3x²

Horizontal translation = 4 (moving right)

Vertical translation = 3 (up)

f(x) = 3(x - 4)² + 3

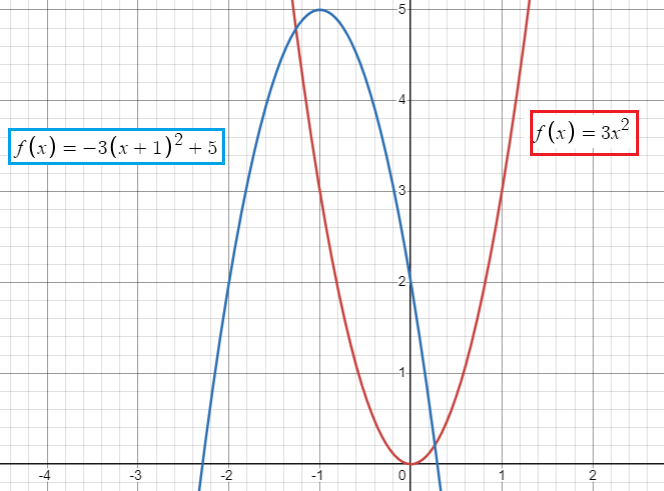
f) a reflection in the x-axis, then a horizontal translation 1 unit to the left, and then a vertical translation 5 units up

• Reflection across x-axis, so put y = -y
• Horizontal translation of 1 unit to the left. So, put h = -1
• Vertical translation of 5 units up. So, put k = 5

f(x) = 3x²

f(x) = -3(x - (-1))² + 5

f(x) = -3(x + 1)² + 5

Problem 2 :

For the graph of f(x) = √x, identify the transformation that would not be applied to f(x) to obtain the graph y = 2f(-2x) + 3

a) Vertical stretch by a factor of 2

b) Reflection in x-axis

c) Vertical translation up 3 units.

d) Horizontal compression by factor of 1/2.

Solution :

Given function is f(x) = √x

y = 2f(-2x) + 3

By observing the transformation,

Horizontal compression of 2 units, vertical translation of 3 units up and vertical stretch of 2 units. Along with reflection across y-axis.

So, option b will not work by comparing with the list of transformations.