SEPARATION OF POINTS AND COLLINEAR POINTS

Find the value of x if A, B and C are collinear points and B is between A and C.

Problem 1 :

AB = 6x, BC = x - 5, AC = 23

Solution :

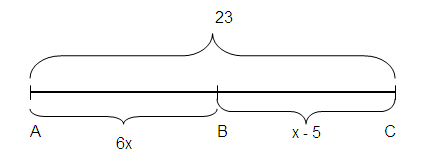
AC = AB + BC

23 = 6x + x - 5

23 = 7x - 5

7x = 23 + 5 

7x = 28

x = 28/7

x = 4

So, the value of x is 4.

Problem 2 :

AB = 5, BC = 3x + 7, AC = 5x - 2

Solution :

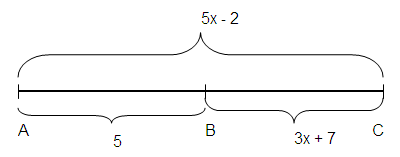
AC = AB + BC

5x - 2 = 5 + 3x + 7

5x - 2 = 3x + 12

5x - 3x = 12 + 2

2x = 14

x = 14/2

x = 7

So, the value of x is 7.

Problem 3 :

AB = 2x, BC = x - 2, AC = 28

Solution :

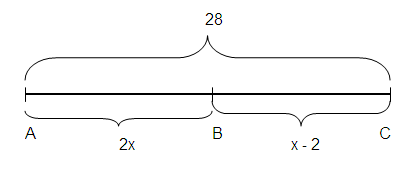
AC = AB + BC

28 = 2x + x - 2

28 = 3x - 2

 3x = 28 + 2

3x = 30

x = 30/3

x = 10

So, the value of x is 10.

Problem 4 :

AB = 3x, BC = 2x - 7, AC = 2x + 35

Solution :

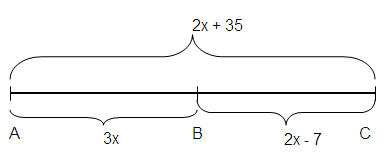
AC = AB + BC

2x + 35 = 3x + 2x - 7

2x + 35 = 5x - 7

 5x  - 2x = 35 + 7

3x = 42

x = 42/3

x = 14

So, the value of x is 14.

Problem 5 :

AB = 5x - 1, BC = 14, AC = 25 - x

Solution :

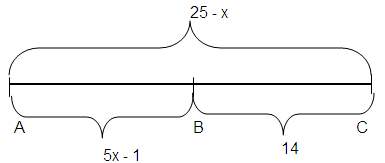
AC = AB + BC

25 - x = 5x - 1 + 14

25 - x = 5x + 13

 5x  + x = 25 - 13

6x = 12

x = 12/6

x = 2

So, the value of x is 2.

Problem 6 :

Find the distance between S and F.

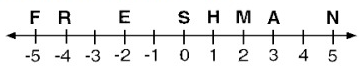
Solution :

Distance between S and F = |-5 - 0|

= |-5|

Distance will not negative. So, |-5| is 5.

Hence, distance between S and F is 5 units.

Problem 7 :

Find the distance between S and H.

Solution :

Distance between S and H = |1 - 0|

= 1

So, distance between S and H is 1 unit.