SEGMENT ADDITION POSTULATE

In order for you to say that a point B is between two points A and C, all three points must lie on the same line, and AB + BC = AC

If B is between A and C then AB + BC = AC

Problem 1 :

What is the measure of

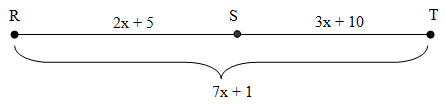
Solution :

S is the point lies on the middle.

Using segment addition postulate, we get

RT = RS + ST

7x + 1 = 2x + 5 + 3x + 10

7x + 1 = 5x + 15

7x - 5x = 15 - 1

2x = 14

x = 7

Problem 2 :

Using the segment addition postulate G is between F and H, FG = 6 and GH = 11. Find FH.

Solution :

G is the point between F and H,

FH = FG + GH

FH = 6 + 11

FH = 17

Problem 3 :

Y is between X and Z, XZ = 8 and XY = 3. Find YZ.

Solution :

XZ = XY + YZ

8 = 3 + YZ

YZ = 8 - 3

YZ = 5

Problem 4 :

Using the segment addition postulate M is between N and O. Find NO.

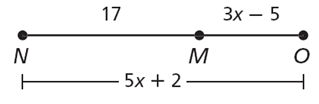
Solution :

NO = NM + MO

5x + 2 = 17 + 3x - 5

5x - 3x = 12 - 2

2x = 10

x = 10/2

x = 5

Finding length of NO :

NO = 5x + 2

NO = 5(5) + 2

NO = 27

Problem 5 :

E is between D and F. Find DF.

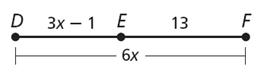
Solution :

DE + EF = DF

3x - 1 + 13 = 6x

3x + 12 = 6x

12 = 6x - 3x

3x = 12

x = 12/3

x = 4

Applying the value of x in DF.

DF = 6(4)

DF = 24

Problem 6 :

D is the midpoint of EF, ED = 4x + 6, and DF = 7x – 9. Find ED, DF, and EF.

Solution :

D is the midpoint of the line segment EF.

ED = DF

4x + 6 = 7x - 9

4x - 7x = -9 - 6

-3x = -15

x = 15/3

x = 5

Problem 7 :

Find CE.

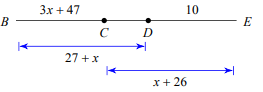
Solution :

BD = BC + CD

27 + x = 3x + 47 + CD

CD = 27 + x - 3x - 47

CD = -2x - 20 ------(1)

CE = CD + DE

x + 26 = CD + 10

CD = x + 26 - 10

CD = x + 16 ------(2)

(1) = (2)

-2x - 20 = x + 16

-2x - x = 16 + 20

-3x = 36

x = -12

Applying the value of x in CE.

CE = x + 26

CE = -12 + 26

CE = 14

Problem 8 :

Solve for x.

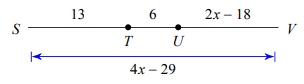
Solution :

SV = ST + TU + UV

4x - 29 = 13 + 6 + 2x - 18

4x - 29 = 1 + 2x

4x - 2x =1 + 29

2x = 30

x = 15

Problem 9 :

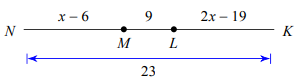
Solution :

NK = NM + ML + LK

23 = x - 6 + 9 + 2x - 19

23 = 3x + 3 - 19

23 = 3x - 16

23 + 16 = 3x 

x = 39/3

x = 13

Problem 10 :

Find the length of BD.

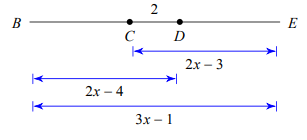
Solution :

BE = BC + CD + DE

BD = BC + CD

2x - 4 = BC + 2

2x - 4 - 2 = BC

BC = 2x - 6 ----(1)

CE = DC + DE

2x - 3 = 2 + DE

DE = 2x - 3 - 2

DE = 2x - 5 ----(2)

BE = 2x - 6 + 2 + 2x - 5

Applying the value of BE

3x - 1 = 4x - 4 - 5

3x - 4x = -9 + 1

-x = -8

x = 8

Finding the length of BD :

BD = BC + CD

BD = 2x - 6 + 2

BD = 2x - 4

Applying the value of x, we get

BD = 2(8) - 4

BD = 12