RULES FOR 90 DEGREE AND 270 DEGREE ROTATION

Find the coordinates of the vertices of each figure after the given transformation.

Problem 1 :

rotation 90° counterclockwise about the origin

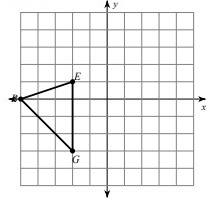
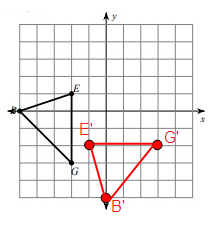
Solution:

Given,

B(-5, 0), E(-2, 1) and G(-2, -3)

Here, triangle is rotated 90° counterclockwise. So, the rule that we have to apply here is

(x, y) ---> (-y, x)

B(-5, 0) = B'(0, -5)

E(-2, 1) = E'(-1, -2)

G(-2, -3) = G'(3, -2)

Vertices of the rotated figure are

B'(0, -5), E'(-1, -2) and G'(3, -2)

Problem 2 :

rotation 90° counterclockwise about the origin

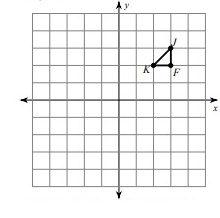
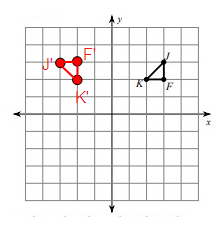
Solution:

Given,

J(3, 3), K(2, 2) and F(3, 2)

Here, triangle is rotated 90° counterclockwise. So, the rule that we have to apply here is

(x, y) ---> (-y, x)

J(3, 3) = J'(-3, 3)

K(2, 2) = K'(-2, 2)

F(3, 2) = F'(-2, 3)

Vertices of the rotated figure are

J'(-3, 3), K'(-2, 2) and F'(-2, 3)

Problem 3 :

rotation 90° clockwise about the origin

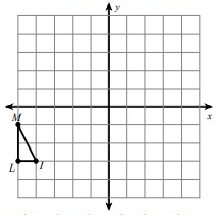
Solution:

Given, M(-5, -1), L(-5, -3) and I(-4, -3)

Here, triangle is rotated 90° clockwise. So, the rule that we have to apply here is

(x, y) ---> (y, -x)

M(-5, -1) = M'(-1, 5)

L(-5, -3) = L'(-3, 5)

I(-4, -3) = I'(-3, 4)

Vertices of the rotated figure are

M'(-1, 5), L'(-3, 5), I'(-3, 4) 

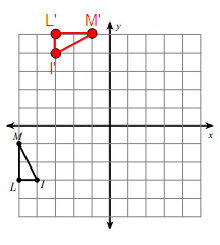
Problem 4 :

rotation 90° clockwise about the origin

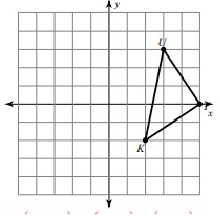
Solution:

Given, U(3, 3), T(5, 0) and K(2, -2)

Here, triangle is rotated 90° clockwise. So, the rule that we have to apply here is

(x, y) ---> (y, -x)

U(3, 3) = U'(3, -3)

T(5, 0) = T'(0, -5)

K(2, -2) = K'(-2, -2)

Vertices of the rotated figure are

U'(3, -3), T'(0, -5) and K'(-2, -2) 

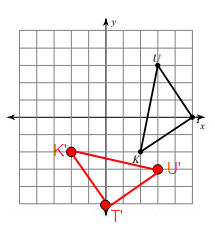
Rotate each shape as described.

Problem 5 : 

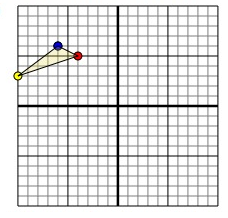
The shape above has the following coordinates:

A (-4, 5), B (-10, 3) and C (-6, 6)

Rotate the shape 270° clockwise.

Solution:

Here, triangle is rotated 270° clockwise. So, the rule that we have to apply here is

(x, y) ---> (-y, x)

A(-4, 5) = A'(-5, -4)

B(-10, 3) = B'(-3, -10)

C(-6, 6) = C'(-6, -6)

Vertices of the rotated figure are

A'(-5, -4), B'(-3, -10) and C'(-6, -6) 

Problem 6 :

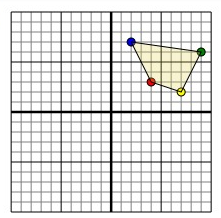
The shape above has the following coordinates:

A (4, 3), B (7, 2), C (9, 6) and D (2, 7)

Rotate the shape 270° clockwise.

Solution:

Here, triangle is rotated 270° clockwise. So, the rule that we have to apply here is

(x, y) ---> (-y, x)

A(4, 3) = A'(-3, 4)

B(7, 2) = B'(-2, 7)

C(9, 6) = C'(-6, 9)

D(2, 7) = D'(-7, 2)

Vertices of the rotated figure are

A'(-3, 4), B'(-2, 7), C'(-6, 9) and D'(-7, 2)

Problem 7 :

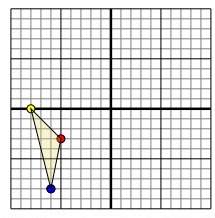
The shape above has the following coordinates:

A (-5, -3), B (-8, 0) and C (-6, -8)

Rotate the shape 270° counter-clockwise.

Solution:

Here, triangle is rotated 270° counter-clockwise. So, the rule that we have to apply here is

(x, y) ---> (y, -x)

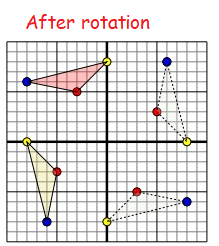
A(-5, -3) = A'(-3, 5)

B(-8, 0) = B'(0, 8)

C(-6, -8) = C'(-8, 6)

Vertices of the rotated figure are

A'(-3, 5), B'(0, 8) and C'(-8, 6) 

Problem 8 :

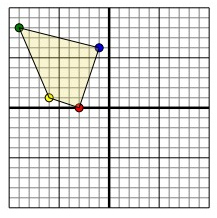
The shape above has the following coordinates:

A(-3, 0), B (-6, 1), C (-9, 8) and D (-1, 6)

Rotate the shape 90° clockwise.

Solution:

Here, triangle is rotated 90° clockwise. So, the rule that we have to apply here is

(x, y) ---> (y, -x)

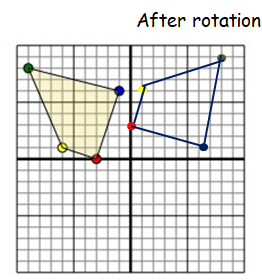
A(-3, 0) = A'(0, 3)

B(-6, 1) = B'(1, 6)

C(-9, 8) = C'(8, 9)

D(-1, 6) = D'(6, 1)

Vertices of the rotated figure are

A'(0, 3), B'(1, 6), C'(8, 9) and D'(6, 1)