ROTATIONS IN THE COORDINATE PLANE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Rotating the shape means moving them around a fixed point. There are two directions
i) Clockwise
ii) Counter clockwise (or) Anti clockwise
The shape itself stays exactly the same, but its position in the space will change.
|
90° clockwise 90° counter clockwise 180° 270° clockwise 270° counter clockwise |
(x, y) ==> (y, -x) (x, y) ==> (-y, x) (x, y) ==> (-x, -y) (x, y) ==> (-y, x) (x, y) ==> (y, -x) |
Problem 1 :
Rotate the following points 90º counterclockwise about the origin on the coordinate plane below.
|
a) A(-2, -5) A’(__, ___) |
b) A(-4, 1) A’(__, ___) |
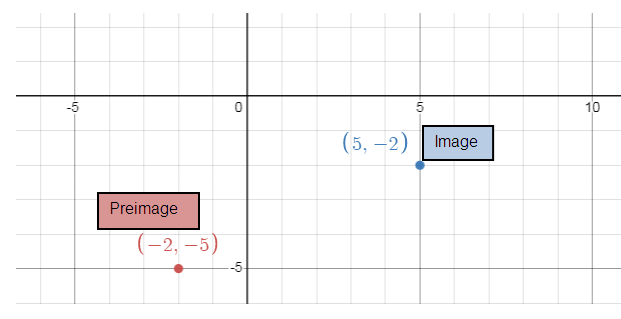
c) In the graphs above connect the pre – image point A to the origin. Then connect the origin to the image point A’. What angle has been formed ?
Solution :
a) 90º counterclockwise (x, y) = (-y, x)
A(-2, -5) A'(5, -2)
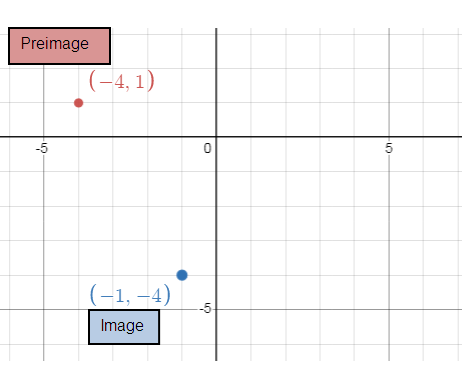
b) 90º counterclockwise (x, y) = (-y, x)
B(-4, 1) B'(-1, -4)
c) So, the angle has been formed 360º.
Problem 2 :
Rotate the following points 180º.
|
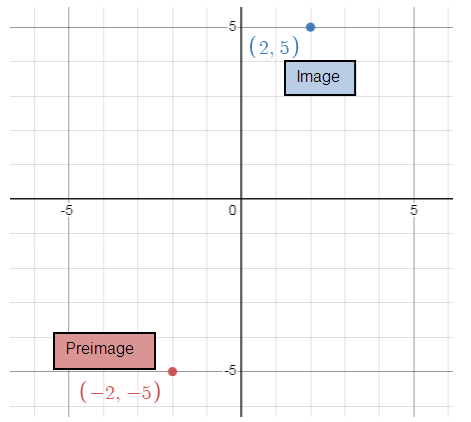
a) B(-2, -5) B’( , ) |
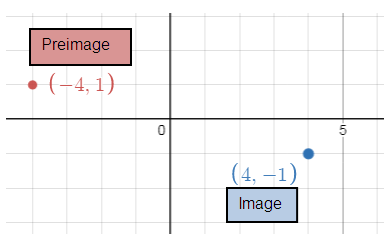
b) B(-4, 1) B’( , ) |
c) In the graphs above connect the pre – image point B to the origin. Then connect the origin to the image point B’. What angle has been formed ?
Solution :
a) (x, y) = (-x, -y)
B(-2, -5) B'(2, 5)
b) (x, y) = (-x, -y)
B(-4, 1) B'(4, -1)
c) So,the angle has been formed is 270º.
Problem 3 :
Rotate the following points 270º counterclockwise.
|
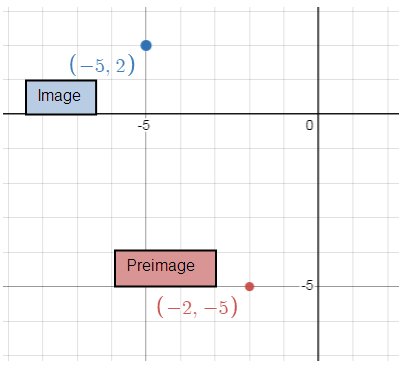
a) C(-2, -5) C’( , ) |
b) C(-4, 1) C’( , ) |
c) In the graphs above connect the pre – image point C to the origin. Then connect the origin to the image point C’. What angle has been formed ?
d) A 270º counterclockwise angle is the same as a ____ clockwise angle.
Solution :
a) 270º counterclockwise (x, y) = (y, -x)
C(-2, -5) C'(-5, 2)
b) (x, y) = (y, -x,)
C(-4, 1) ---> C'(1, 4)
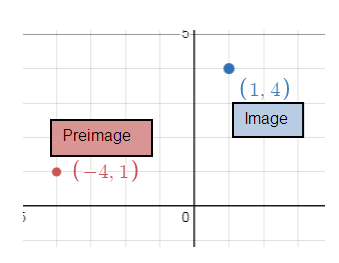
c) So, the angle has been formed is 180º.
d) A 270º counterclockwise angle is the same as a 90º clockwise angle.
Problem 4 :
Rotate the following figure 90º counterclockwise. Write the pre – image and image points in the spaces provided.
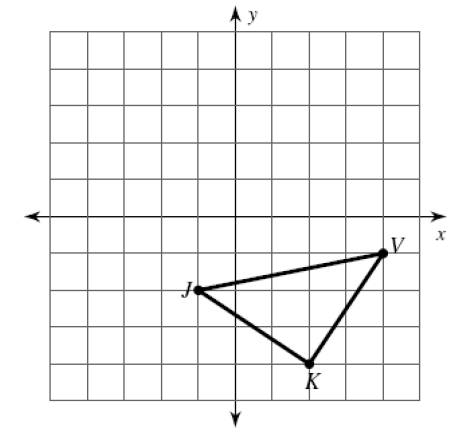
J(-1, -2) ---> J’ (__, ___)
K(__, ___) ---> K’ (__, ___)
V(__, ___) ---> V’ (__, ___)
Solution :
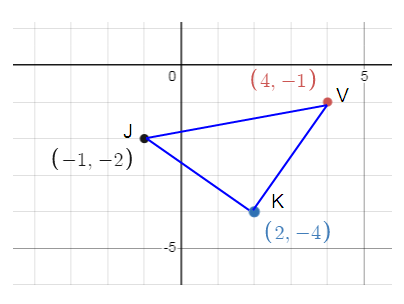
90º counterclockwise. So, (x, y) = (-y, x)
J(-1, -2) --->J'(2, -1)
K(2, -4) ---> K'(4, 2)
V(4, -1) ---> V'(1, 4)
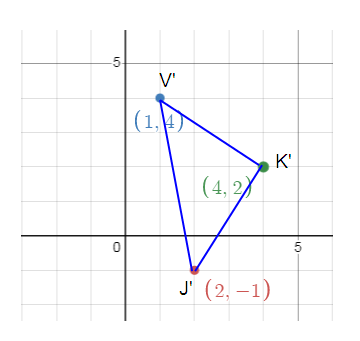
Problem 5 :
Rotate the following figure 180º. Write the pre – image and image points in the spaces provided.
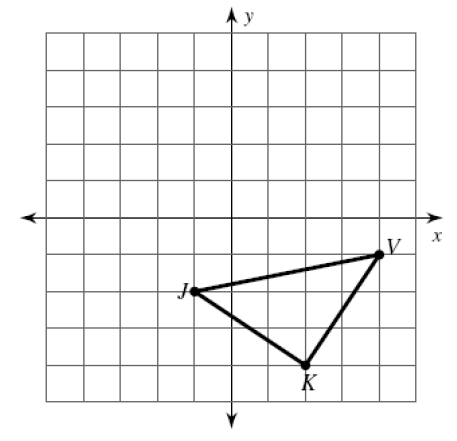
J(-1, -2) ----> J’ (__, ___)
K(__, ___) ----> K’ (__, ___)
V(__, ___) ---> V’ (__, ___)
Solution :
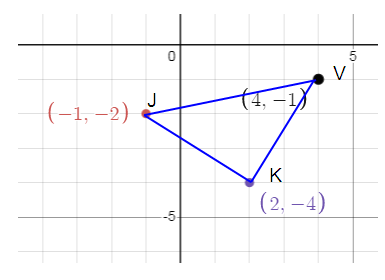
(x, y) = (-x, -y)
J(-1, -2) --->J'(1, 2)
K(2, -4) ---> K'(-2, 4)
V(4, -1) ---> V'(-4, 1)
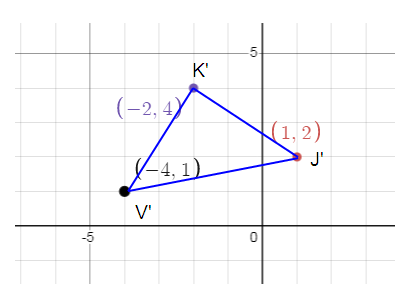
Problem 6 :
Rotate the following figure 270º counterclockwise. Write the pre – image and image points in the spaces provided.
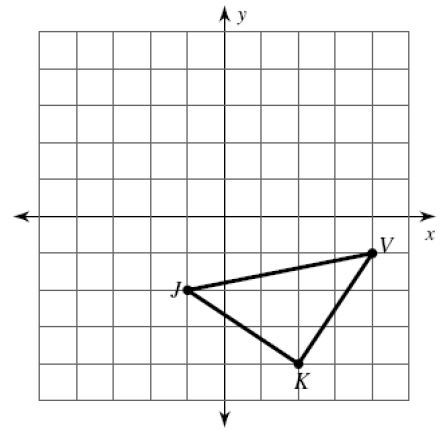
J(-1, -2) ----> J’ (__, ___)
K(__, ___) ----> K’ (__, ___)
V(__, ___) ---> V’ (__, ___)
Solution :
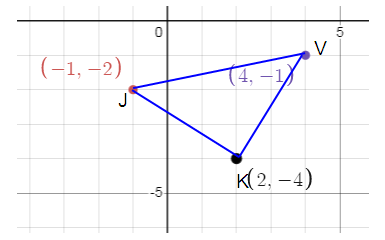
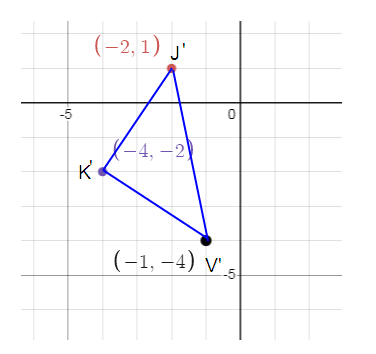
270º counterclockwise. So, (x, y) = (y, -x)
J(-1, -2) --->J'(-2, 1)
K(2, -4) ---> K'(-4, -2)
V(4, -1) ---> V'(-1, -4)
In each of the three graphs below determine how many degrees the shape has been rotated around the origin. (Remember in math everything is counterclockwise.)
Problem 7 :
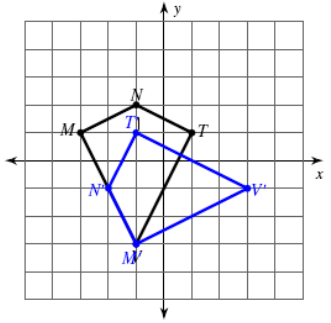
Solution :
N (-1, 2) ----> N'(-2, -1)
M (-3, 1) ---> M' (-1, -3)
V(-1, -3) --->V'(3, -1)
T(1, 1) ----> T'(-1, 1)
The given shape is rotated 90º counter - clockwise about the origin. That's why the coordinates (x, y) became (-y, x).
Problem 8 :
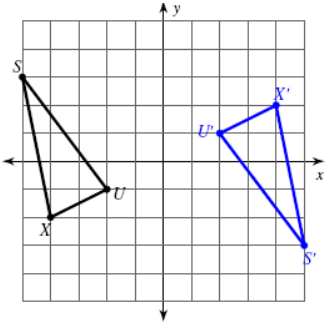
Solution :
X (-4, -2) ----> X'(4, 2)
U (-2, -1) ---> U' (2, 1)
S(5, 3) ---> S'(5, -3)
The shape given above is rotated 180º counter - clockwise about the origin, the coordinates (x, y) become (-x, -y).
Problem 9 :
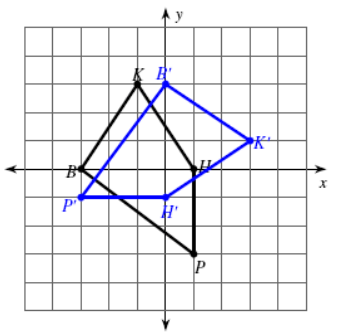
Solution :
B(-3, 0) ----> B'(0, 3)
K (-1, 3) ---> K' (3, 1)
P(1, -3) ---> P'(-3, -1)
H(1, 0) ---> H'(0, -1)
The shape given above is rotated about 270º counter - clockwise about the origin, the coordinates (x, y) become (y, -x).
Problem 10 :
Rotate 90º
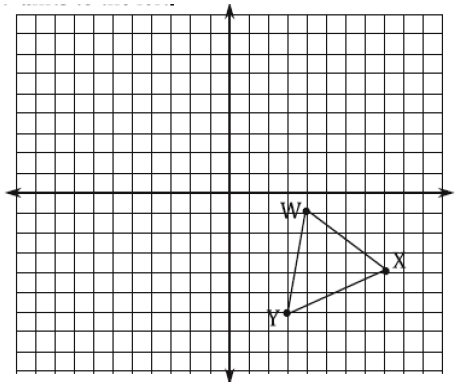
W(__, ___) ----> W’ (__, ___)
X(__, ___) ----> X’ (__, ___)
Y(__, ___) ---> Y’(__, ___)
Solution :
By observing the figure,
The triangle rotated 90º clockwise.
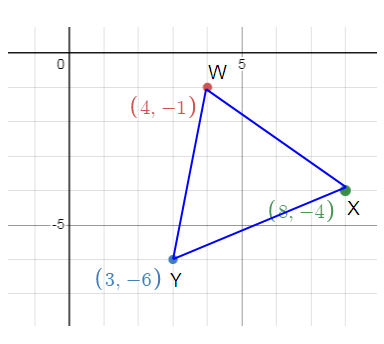
90º clockwise. So, (x, y) = (y, -x)
W(4, -1) ----> W’ (-1, -4 )
X(3, -6) ----> X’ (-6, -3)
Y(8, -4) ---> Y’ (-4, -8)
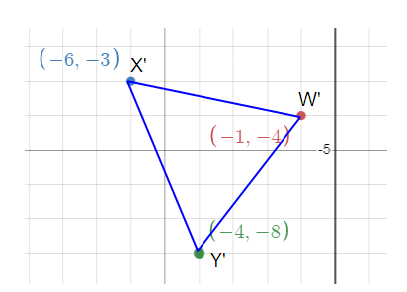
Problem 11 :
Rotate the shape 180º. Then translate the new image 3 left and 1 down.
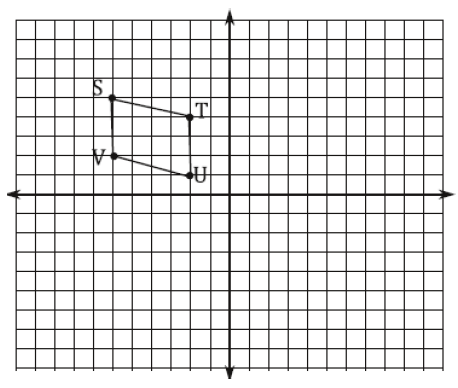
S(__, ___) --> S' (__, ___)
T(__, ___) --> T' (__, ___)
U(__, ___) --> U'(__, ___)
V(__, ___) --> V'(__, ___)
Shade in the final image and label using triple prime notation.
Write the rule for just the translation :
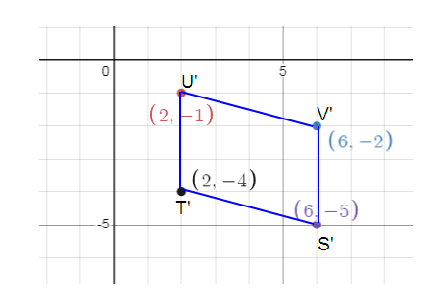
Solution :
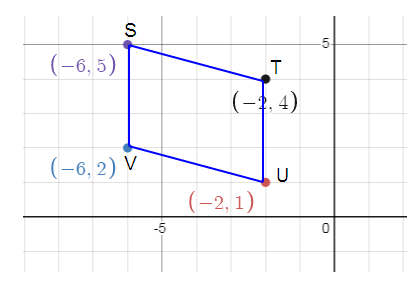
S(-6, 5) S'(6, -5)
T(-2, 4) T'(2, -4 )
U(-2, 1) U'(2, -1 )
V(-6, 2) V'(6, -2 )
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling