ROTATION OF 2D SHAPES WITH CENTER OF ROTATION

If we rotate the 2d shape about origin, we will follow the rules given below about the angle that we are rotating.

Step 1 :

If center of rotation is something else than origin, we have to draw the horizontal and vertical lines in order to consider we have origin at the specified point.

Step 2 :

From the center of rotation, we have to move horizontally and vertically to get each vertices of the 2d shape.

Step 3 :

Moving right, x-coordinate = positive

Moving left, x-coordinate = negative

Moving up, y-coordinate = positive

Moving down, y-coordinate = negative

Rotating the shape means moving them around a fixed point. There are two directions

i) Clockwise

ii) Counter clockwise (or) Anti clockwise

The shape itself stays exactly the same, but its position in the space will change.

90° clockwise

90° counter clockwise

180°

270° clockwise

270° counter clockwise

(x, y) ==> (y, -x)

(x, y) ==> (-y, x)

(x, y) ==> (-x, -y)

(x, y) ==> (-y, x)

(x, y) ==> (y, -x)

Note :

90 degree clockwise rotation and 270 degree counter clockwise direction both are same.

90 degree counter clockwise direction and 270 degree clockwise direction both are same.

Rotate each of the shapes below as instructed, using P as the centre of rotation

Problem 1 :

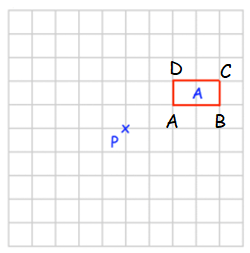
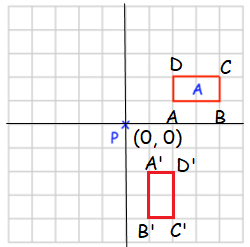
Rotate 90° clockwise about P.

Solution :

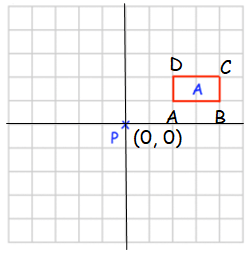
Point A :

From P, move 2 units right and 1 unit up. So, (2, 1)

Point B :

From P, move 4 units right and 1 unit up. So, (4, 1)

Point C :

From P, move 4 units right and 2 unit up. So, (4, 2)

Point D :

From P, move 2 units right and 2 unit up. So, (2, 2)

Rule for 90° clockwise rotation

(x, y) ==> (y, -x)

A (2, 1)

B (4, 1)

C (4, 2)

D (2, 2)

A' (1, -2)

B' (1, -4)

C' (2, -4)

D' (2, -2)

Problem 2 :

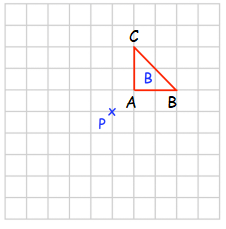
Rotate 90° counter clockwise about P.

Solution :

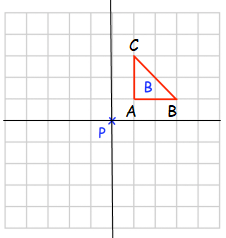
Point A :

From P, move 1 unit right and 1 unit up. So, A(1, 1)

Point B :

From P, move 3 units right and 1 unit up. So, B(3, 1)

Point C :

From P, move 1 unit right and 3 units up. So, C(1, 3)

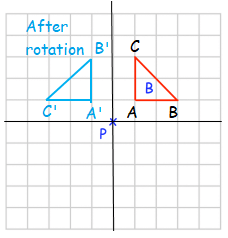
Rule for 90° counter clockwise rotation

(x, y) ==> (-y, x)

A(1, 1)

B(3, 1)

C(1, 3)

A'(-1, 1)

B'(-1, 3)

C'(-3, 1)

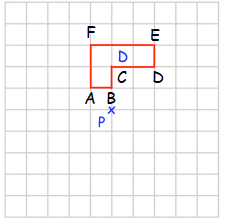
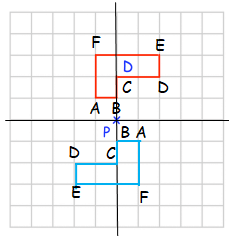
Problem 3 :

Rotate 180° about P.

Solution :

Point A :

From P, move 1 unit left and 1 unit up. So, A(-1, 1)

Point B :

From P, no horizontal move and move up 1 unit. So, B (0, 1)

Point C :

From P, no horizontal move and move up 2 units. So, C (0, 2)

Point D :

From P, 2 units right and 2 units up. So, D (2, 2)

Point E :

From P, 2 units right and 3 units up. So, E (2, 3)

Point F :

From P, 1 unit left and 3 units up. So, F (-1, 3)

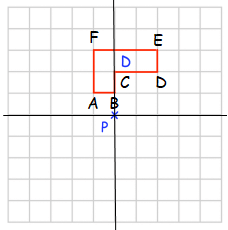
Rule for 180° rotation

(x, y) ==> (-x, -y)

A(-1, 1)

B (0, 1)

C (0, 2)

D (2, 2)

E (2, 3)

F (-1, 3)

A'(1, -1)

B' (0, -1)

C' (0, -2)

D' (-2, -2)

E' (-2, -3)

F' (1, -3)

ROTATION OF 2D SHAPES WITH CENTER OF ROTATION

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling