ROTATION OF 2D SHAOES PRACTICE PROBLEMS

Problem 1 :

Rotate the following points 90° counterclockwise about the origin on the coordinate plane below.

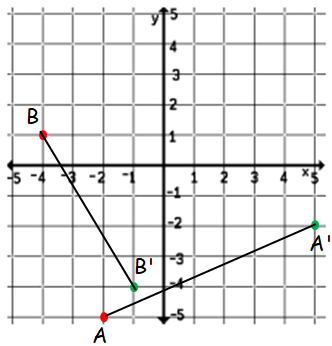
a)  A(-2,-5)  --> A’( __, ___ )

b) B (-4, 1)  --> B’( __, ___ )

c) In the graphs above connect the pre-image point A to the origin. Then connect the origin to the image point A’. What angle has been formed?

Solution :

Rule for 90 degree counter clockwise direction.

(x, y) ==> (-y, x)

Rotation of A(-2,-5) about 90 degree counter clockwise direction :

x = -2, y = -5 then -y = 5

A(-2,-5)  --> A’(5, -2)

b) B (-4, 1)  --> B’( __, ___ ).

Rotation of A(-4,1) about 90 degree counter clockwise direction :

x = -4, y = 1 then -y = -1

(x, y) ==> (-y, x)

B(-4, 1)  --> B’(-1, -4)

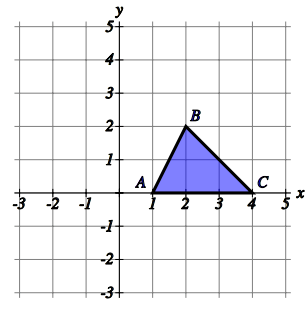
Problem 2 :

Rotate the triangle ABC 90° anti-clockwise about centre (0,0). Give the coordinates of the image points A, B and C

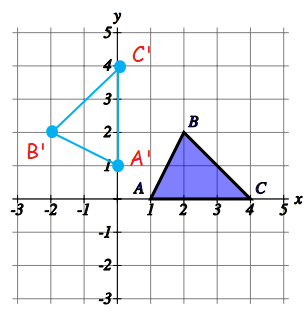
Solution :

Let us mark the coordinates A(1, 0), B(2, 2) and C(4, 0)

Rule for 90 degree counter clock wise rotation :

(x, y) ==> (-y, x)

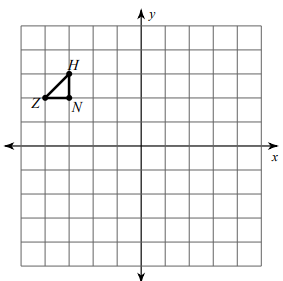
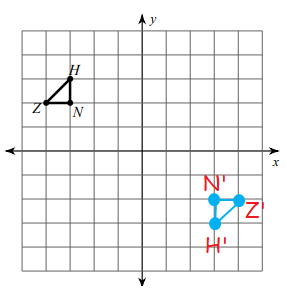
Problem 3 :

Rotate the figure as indicated. Label the image using prime notation.

rotation 180° about the origin

Solution :

Let us mark the coordinates,

N(-3, 2) H(-3, 3) and Z(-4, 2)

Rule for 180 rotation :

(x, y) ==> (-x, -y)

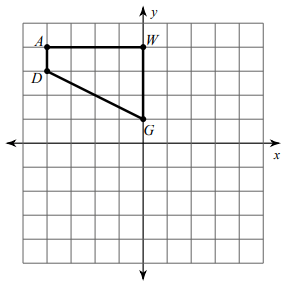
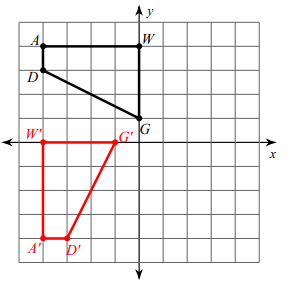
Problem 4 :

rotation 90° counterclockwise about the origin

Solution :

Let us mark the coordinates in the original picture.

A(-4, 4) D(-4, 3) G(0, 1) and W(0, 4)

Rules for 90 degree counter clockwise rotation :

(x, y) ==> (-y, x)

Problem 5 :

Find the coordinates of the vertices of each figure after the given transformation.

rotation 180° about the origin

E(2, −2), J(1, 2), R(3, 3), S(5, 2)

Solution :

Rule for rotation of 180 :

(x, y) ==> (-x, -y)