ROTATING THE SHAPE AROUND THE CENTER

If we rotate the 2d shape about origin, we will follow the rules given below about the angle that we are rotating.

Step 1 :

If center of rotation is something else than origin, we have to draw the horizontal and vertical lines in order to consider we have origin at the specified point.

Step 2 :

From the center of rotation, we have to move horizontally and vertically to get each vertices of the 2d shape.

Step 3 :

Moving right, x-coordinate = positive

Moving left, x-coordinate = negative

Moving up, y-coordinate = positive

Moving down, y-coordinate = negative

Rotating the shape means moving them around a fixed point. There are two directions

i) Clockwise

ii) Counter clockwise (or) Anti clockwise

The shape itself stays exactly the same, but its position in the space will change.

90° clockwise

90° counter clockwise

180°

270° clockwise

270° counter clockwise

(x, y) ==> (y, -x)

(x, y) ==> (-y, x)

(x, y) ==> (-x, -y)

(x, y) ==> (-y, x)

(x, y) ==> (y, -x)

Problem 1 :

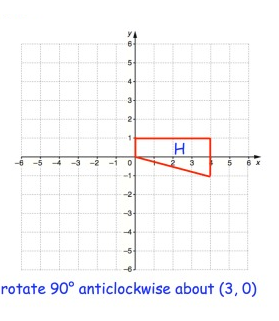
Solution:

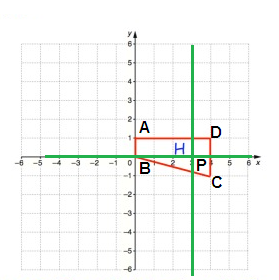
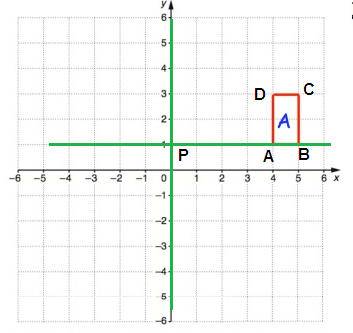
Point A:

From P, move 3 units left and 1 unit up. So, A(-3, 1)

Point B :

From P, move 3 units left and no vertical movement. So, B(-3, 0)

Point C :

From P, move 1 unit right and 1 unit down. So, C(1, -1)

Point D :

From P, move 1 unit right and 1 unit up. So, D(1, 1)

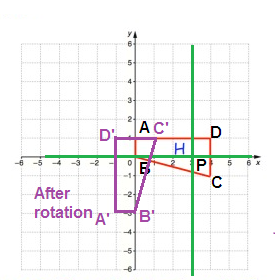
Rule for 90° anti clockwise rotation

(x, y) ==> (-y, x)

A(-3, 1)

B(-3, 0)

C(1, -1)

D(1, 1)

A'(-1, -3)

B'(0, -3)

C'(1, 1)

D'(-1, 1)

Problem 2 :

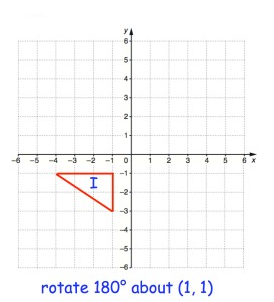
Solution:

Point A:

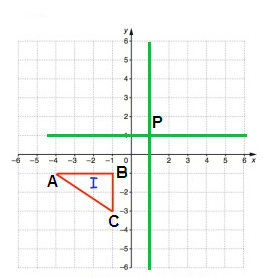
From P, move 5 units left and 2 units down. So, A(-5, -2)

Point B :

From P, 2 unit left and 2 units down. So, B(-2, -2)

Point C :

From P, 2 units left and 4 units down. So, C(-2, -4)

Rule for 180° rotation

(x, y) ==> (-x, -y)

A(-5, -2)

B(-2, -2)

C(-2, -4)

A'(5, 2)

B'(2, 2)

C'(2, 4)

Problem 3 :

Solution:

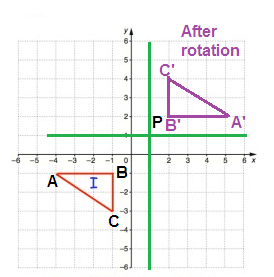
Point A :

From P, move 4 units right and no vertical movement. So, A(4, 0)

Point B :

From P, move 5 units right and no vertical movement. So, B(5, 0)

Point C :

From P, move 5 units right and 2 units up. So, C(5, 2)

Point D :

From P, move 4 units right and 2 units up. So, A(4, 2)

Rule for 90°counter clockwise rotation

(x, y) ==> (-y, x)

A(4, 0)

B(5, 0)

C(5, 2)

D(4, 2)

A'(0, 4)

B(0, 5)

C(-2, 5)

D(-2, 4)

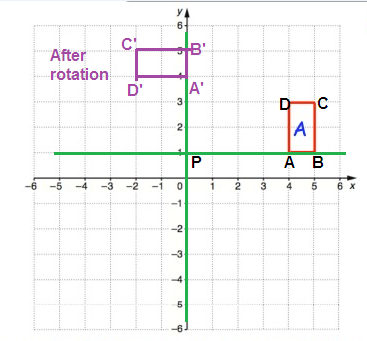
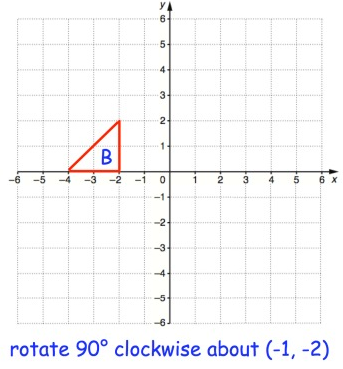
Problem 4 :

Solution:

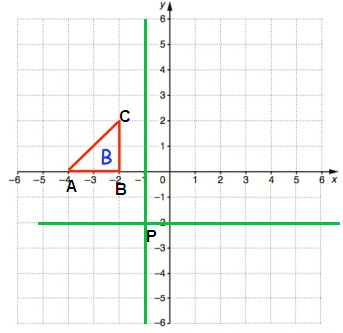
Point A :

From P, move 3 units left and 2 units up. So, A(-3, 2)

Point B :

From P, move 1 unit left and 2 units up. So, B(-1, 2)

Point C :

From P, move 1 unit left and 4 units up. So, C(-1, 4)

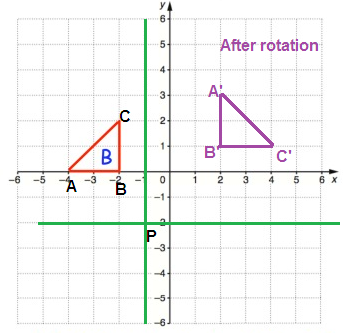
Rule for 90° clockwise rotation

(x, y) ==> (y, -x)

A(-3, 2)

B(-1, 2)

C(-1, 4)

A'(2, 3)

B'(2, 1)

C'(4, 1)

ROTATING THE SHAPE AROUND THE CENTER

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling