RRIGHT TRIANGLE TRIGONOMETRY SAT QUESTIONS

Problem 1 :

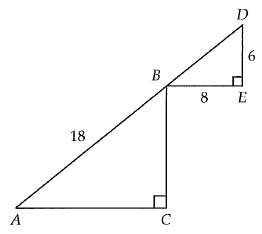
In the figure above, points A, B and D lie on the same line. If AB = 18, BE = 8 and DE = 6. What is the value of sin A ?

Solution :

In triangle BED,

BD² = BE² + ED²

BD² = 8² + 6²

= 64 + 36

BD² = 100

BD = 10

Triangles BDE and ABC are similar.

∠BAC and ∠DBE are corresponding angles.

sin A = sin B

sin B = 6/10

sin B = 0.6

sin A = 0.6

Problem 2 :

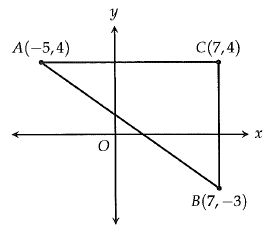
Right triangle ABC is shown in the xy-plane above. What is the value of tan A ?

a)  7/12    b)  3/4      c)  7/9     d)  12/7

Solution :

tan A = Opposite side / Adjacent side

AB = hypotenuse, AC = adjacent side and BC = opposite side

BC = √(7-7)² + (-3-4)²

= √0² + (-7)²

BC = 7

AC = √(-5-7)² + (4-4)²

= √(-12)² + 0²

AC = 12

tan A = 7/12

So, option a is correct.

Problem 3 :

Given the right triangle above, which of the following is equal to a ?

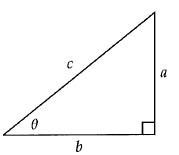
a)  a tan θ    b)  b sin θ      c)  c sin θ     d)  c cos θ

Solution :

a = opposite side, c = hypotenuse and b = adjacent side

sin θ = opposite side / hypotenuse 

sin θ = a / c

c sin θ = a

So, option c is correct.

Problem 4 :

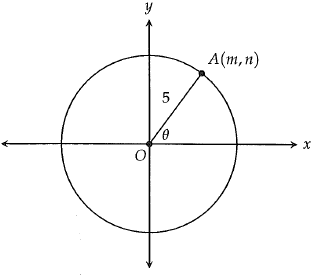
In the xy plane above, a circle with radius 5 has its center at the origin. Point A lies on the circle and has coordinates (m, n). What is n in terms of θ?

a)  5 sin θ    b)  5 cos θ      c)  tan θ     d)  5(sin θ + cos θ)

Solution :

While drawing a perpendicular line from A, we will get a right triangle.

n is the y-coordinate = adjacent side

cos θ = adjacent side / hypotenuse

cos θ = n/5

5 cos θ = n

So, the value of n is 5 cos θ.

Problem 5 :

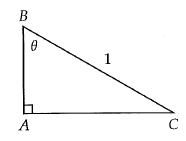
Given right triangle ABC above, which of the following gives the length of AB in terms of θ ?

a)  sin θ   b)  cos θ     c) tan θ      d) 1/sin θ

Solution :

AC - Opposite side, AB - adjacent side and BC - hypotenuse

Here we have to find adjacent side and the known side is hypotenuse.

cos θ = adjacent side / hypotenuse

cos θ = AB / BC

cos θ = AB/1

AB = cos θ

So, option b is correct.

Problem 6 :

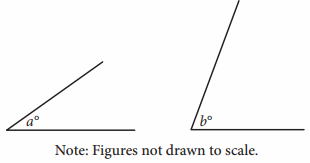
The angles shown above are acute and

sin(a°) = cos( b°).

If a = 4k − 22 and b = 6k − 13 , what is the value of k ?

A) 4.5      B) 5.5     C) 12.5      D) 21.5

Solution :

sin(a°) = cos( b°)

sin(a°) = sin (90 - b°)

a and b are complementary angles.

4k - 22 + 6k -13 = 90

10k - 35 = 90

10k = 125

k = 125/10

k = 12.5

Problem 7 :

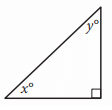
In the triangle above, the sine of x° is 0.6. What is the cosine of y° ?

Solution :

sin x° = 0.6

sin x° = Opposite side / hypotenuse

Opposite side = 0.6, hypotenuse = 1

Adjacent side = √1² - (0.6)²

= √1 - 0.36

= √0.64

= 0.8

cos y = adjacent side / hypotenuse

= 0.8/1

cos y = 0.8

Problem 8 :

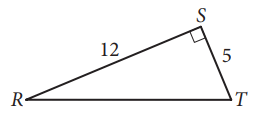
In triangle RST above, point W (not shown) lies on RT. What is the value of cos (∠RSW) − sin (∠WST) ?

Solution :

Given that cos (∠RSW) − sin (∠WST) ---(1)

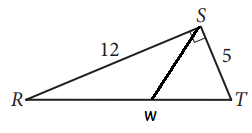
cos (∠RSW) + sin (∠WST) = 90

cos θ = sin (90 - θ)

cos (∠RSW) = sin (90 - ∠RSW)

cos (∠RSW) = sin (∠WST)

Applying the value in (1), we get

= sin (∠WST) − sin (∠WST)

= 0

Problem 9 :

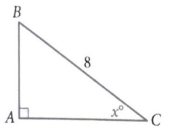
In right triangle ABC above, BC = 8. If cosine x is √3/2, what is the length of AB ?

Solution :

cosine x = √3/2

AB = Opposite side, AC = Adjacent side and BC = hypotenuse

cosine x = √3/2

AC/BC = √3/2

AC/8 = √3/2

AC = (√3/2) x 8

AC = 4√3

Problem 10 :

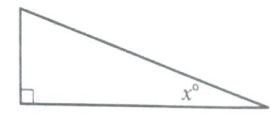
In the figure above, sin (90 - x) = 12/13. What is the value of sin x ?

a)  12/13      b)  5/13      c)  5/12     d)  13/12

Solution :

sin (90 - x) = 12/13

cos x = 12/13 = Adjacent side / Hypotenuse

Opposite side = √13² - 12²

= √169 - 144

= √25

= 5

sin x = 5/13

Problem 11 :

If sin x = a, which of the following must be true for all values of x ?

a) cos x = a     b)  sin (90 - x) = a     c) cos(90 - x) = a

d)  sin (x²) = a²

Solution :

sin x = a

cos(90 - x) = a

So, option c is correct.