RELATED RATE OF CHANGE WORD PROBLEMS

Problem 1 :

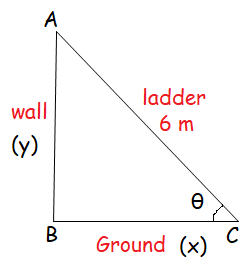
Brian is standing on a 6-meter ladder that is leaning against a wall when Roger begins to pull the bottom of the ladder out away from the wall. The bottom of the ladder is pulled at a constant rate of 0.5 m/s.

a. How fast is the top of the ladder moving when it is 5 meters up the wall?

b. How fast is the angle formed between the ladder and ground changing at this instant?

Solution

Problem 2 :

The radius of a sphere is increasing at a constant rate of 2 in/min. Find the rate of change of the volume of the sphere when the radius is 6 inches and 24 inches

Solution

Problem 3 :

A point is moving along the graph of y =√x in a manner such that dx/dt = 3 cm/sec. Find dy/dt, when x = 4.

Solution

Problem 4 :

Find the rate of change of the distance between the origin and a point moving on the graph of y = sinx if the rate of change of the x-coordinate with respect to time at x = π  is 2 cm/sec.

Solution

Problem 5 :

All edges of a cube are expanding at a rate of 3 cm/sec. How fast is the volume changing when each edge of the cube is 10 cm? How fast is the surface area of the cube changing at this instant?

Solution

Problem 6 :

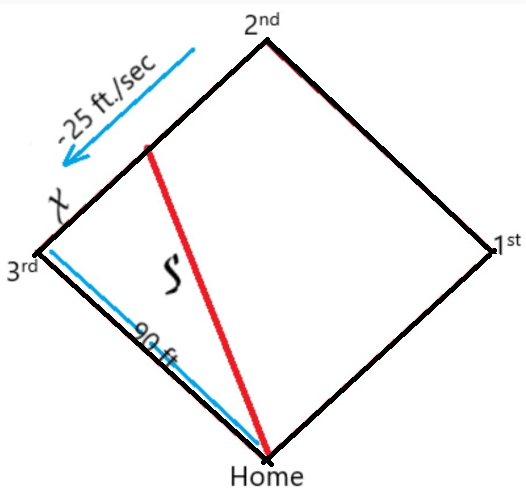
A baseball diamond has the shape of a square with sides 90 feet long (see figure). A player running from second base to third base at a speed of 28 feet per second is 30 feet from third base. At what rate is the player’s distance, s, from home plate changing?

Solution

Problem 7 :

A balloon rises at a rate of 30 meters per second from a point on the ground 30 meters from an observer. Find the rate of change of the angle of elevation of the balloon from the observer when the balloon is 30 meters above the ground.

Solution :

Solution

Problem 8 :

Water is flowing into a cone at a rate of 2 cm³/min. The cone has a height of 16 cm and a radius of 4 cm. How fast is the water level rising when it is

(a) 5 cm deep and (b) 10 cm deep?

Solution