REFLECTION IN COORDINATE PLANE

Problem 1 :

Graph and write the coordinates of the image of point P(5, -4) under each transformation:

a) a reflection in the x-axis: ( __ , __ )

b) a reflection in the y-axis: ( __ , ___)

c) a translation that moves the point 3 units to the left and 6 units up: ( , )

Solution:

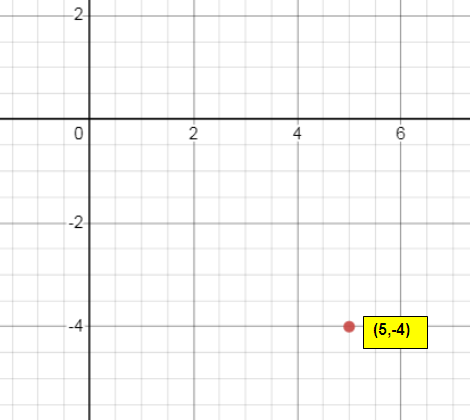
a.

The rule of reflection about x-axis is

(x, y) ==> (x, -y)

(5, -4) ==> (5, 4)

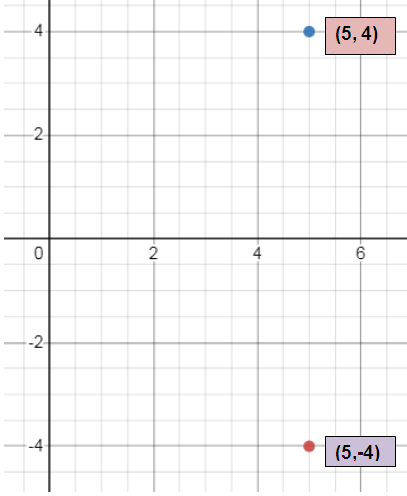
b.

The rule of reflection about y-axis is

(x, y) ==> (-x, y)

(5, -4) ==> (-5, -4)

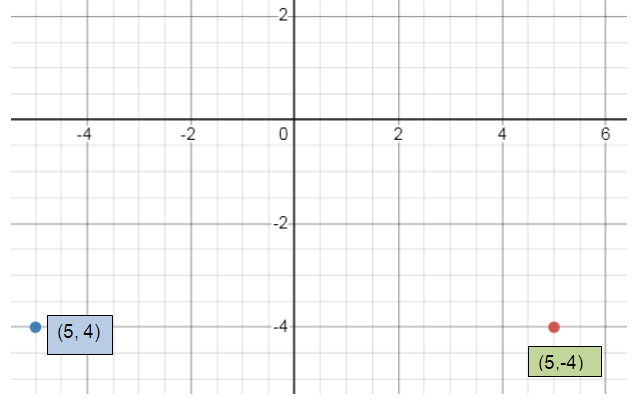
c. 

Let the new origin be (h, k) = (-3, 6) and (x, y) = (5, -4)

Therefore new coordinates (X, Y).

x = X + h and y = Y + k

5 = X - 3 and -4 = Y + 6

X = 8 and Y = -10

Hence, the new coordinates are (8, -10).

Problem 2 :

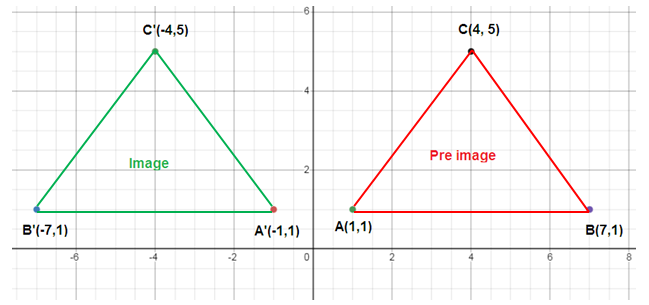
On the grid below, draw △ABC whose vertices are A(1, 1), B(7, 1), and C(4, 5).

a) Draw △A'B'C', the image of △ABC under a reflection in the y-axis.

b) Write the coordinates of A', B', and C':

A' (     )     B' (     )     C' (     )

Solution:

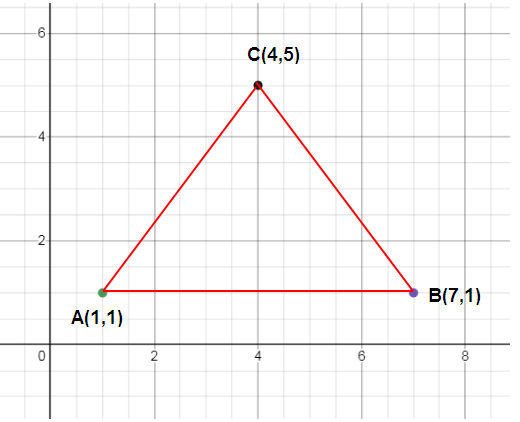
The coordinates of the vertices are

A (1, 1), B (7, 1) and C (4, 5)

A (1, 1) ==> A’ (-1, 1)

B (7, 1) ==> B’ (-7, 1)

C (4, 5) ==> C’ (-4, 5)

Problem 3 :

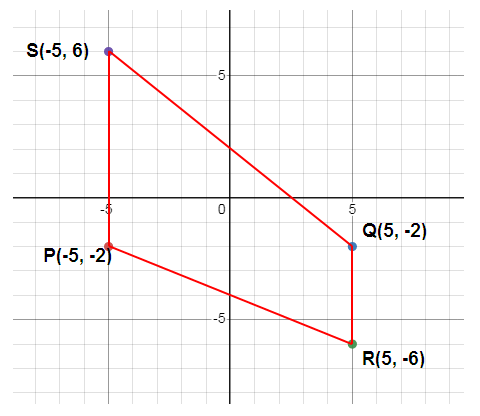
Draw rectangle PQRS whose vertices are P(-5, -2), Q(5, -2), R(5, -6) and S(-5, 6). What are the coordinates of the vertices of rectangle P'Q'R'S', the image of the original rectangle after a reflection in the x-axis?

Solution:

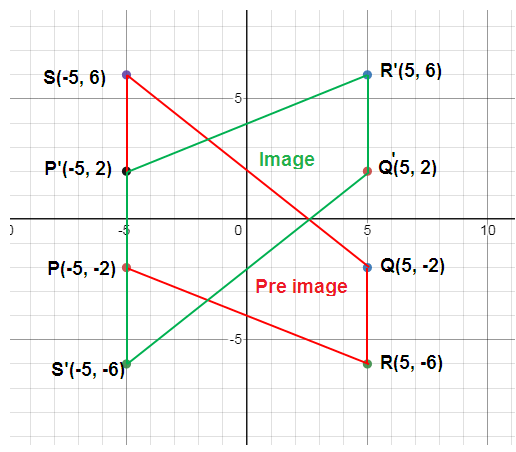
The coordinates of the vertices are

P (-5, -2), Q (5, -2), R (5, -6) and S (-5, 6)

P (-5, -2) ==> P’ (-5, 2)

Q (5, -2) ==> Q’ (5, 2)

R (5, -6) ==> R’ (5, 6)

S (-5, 6) ==> S' (-5, -6)

Problem 4 :

Another word for the point (0, 0) is the ______.

Solution:

Another word for the point (0, 0) is the origin.

Problem 5 :

a. A short hint word to describe translations is a "_____".

b. A short hint word to describe reflections is a "_____".

Solution :

a) T_{(x + h, y + k)}

b) T_x-axis and Ty-axis

Problem 6 :

Another way of writing "reflection in the y-axis" is ______.

Solution :

T_{(x, y)} ==> T'_{(-x, y)}

Problem 7 :

A shortcut way of writing the following translation:

(x, y) --> (x - 1, y + 2) is _____.

Solution :

T_{(-1, 2)}

Problem 8 :

True or False :

Translations preserve congruence of the original image.

Solution :

True

Problem 9 :

True or False (circle one):

Reflections preserve congruence of the original image.

Solution :

True