REFLECTION ACROSS Y EQUAL NEGATIVE X

Reflection about y = -x

The rule of reflection about y = -x is

(x, y) ==> (-y, -x)

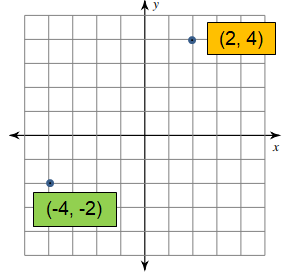
What is preimage ?

Preimage In a transformation, the original figure is called the preimage.

What is image ?

Image In a transformation, the final figure is called the image.

Reflections can be performed easily in the coordinate plane using the general rules below.

Graph the image of the figure using the transformation given.

Problem 1 :

Reflection across the line y = -x.

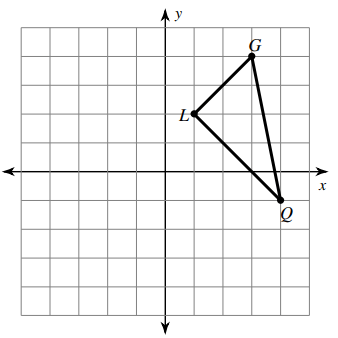
Solution :

By observing the coordinates of the vertices of the triangle given above.

L (1, 2), G (3, 4) and Q (4, -1)

Rule for reflection across y = -x :

(x, y) ==> (-y, -x)

Find the coordinates of the vertices of each figure after the given transformation.

Problem 2 :

Reflection across the y = -x

T(2, 2), C(2, 5), Z(5, 4), F(5, 0)

Solution :

T(2, 2), C(2, 5), Z(5, 4), F(5, 0)

Rule for reflection across y = -x :

(x, y) ==> (-y, -x)

T (2, 2)  ==> T' (-2, -2)

C (2, 5) ==> C' (-5, -2)

Z (5, 4) ==> Z' (-4, -5)

F (5, 0) ==> F (0, -5)

Find the coordinates of the vertices of each figure after the given transformation.

Problem 3 :

Reflection across the line y = -x.

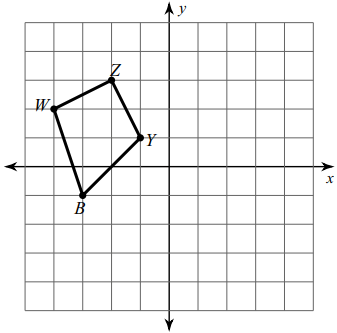
Solution :

By observing the figure, the coordinates are 

W (-4, 2), B (-3, -1), Y (-1, 1), Z (-2, 3)

Rule for reflection across y = -x :

(x, y) ==> (-y, -x)

W (-4, 2)  ==> W' (-2, 4)

B (-3, -1) ==> B' (1, 3)

Y (-1, 1) ==> Y' (-1, 1)

Z (-2, 3) ==> Z' (-3, 2)

Graph the image of the figure using the transformation given.

Problem 4 :

Reflection across the line y = -x.

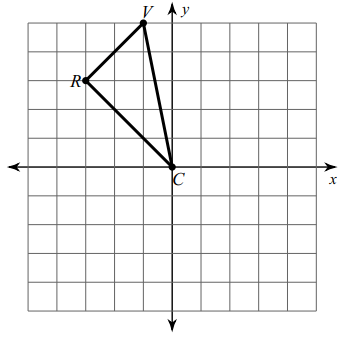
Solution :

By observing the figure, the coordinates are 

R (-3, 3), C (0, 0), V (-1, 5)

Rule for reflection across y = -x :

(x, y) ==> (-y, -x)

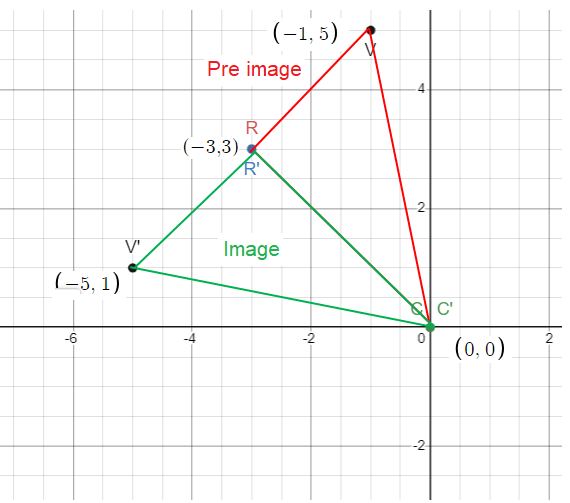
R (-3, 3)  ==> R' (-3, 3)

C (0, 0) ==> C' (0, 0)

V (-1, 5) ==> V' (-5, 1)

Problem 5 :

Reflection across the line y = -x.

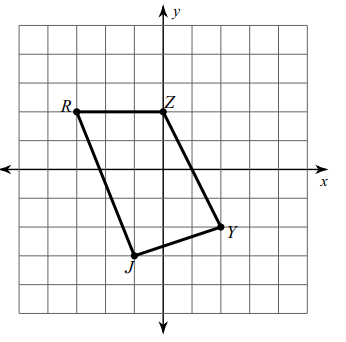
Solution :

By observing the figure, the coordinates are 

J (-1, -3), R (-3, 2), Z (0, 2) and Y (2, -2)

Rule for reflection across y = -x :

(x, y) ==> (-y, -x)

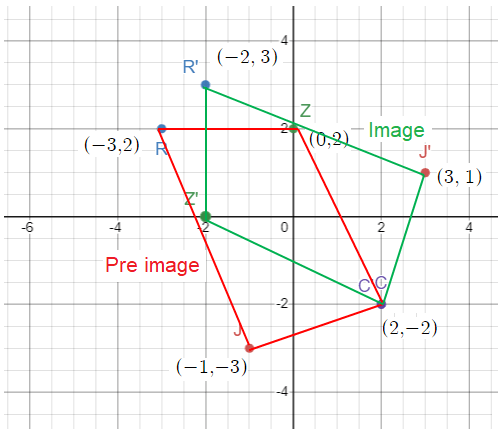
J (-1, -3)  ==> J' (3, 1)

R (-3, 2) ==> R' (2, 3)

Z (0, 2) ==> Z' (-2, 0)

Y (2, -2)  ==> Y' (2, -2)