REFLECTION ACROSS THE Y AXIS

Reflection over y-axis

The rule of reflection about y-axis is

(x, y) ==> (-x, y)

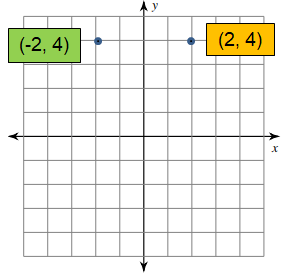
What is preimage ?

Preimage In a transformation, the original figure is called the preimage.

What is image ?

Image In a transformation, the final figure is called the image.

Graph the image of the figure using the transformation given.

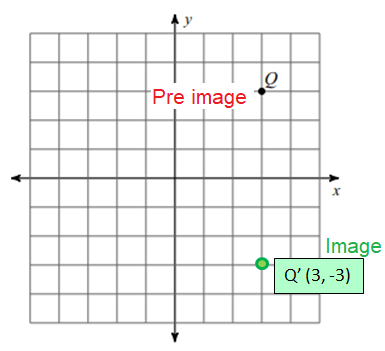
Problem 1 :

Reflection across the y-axis

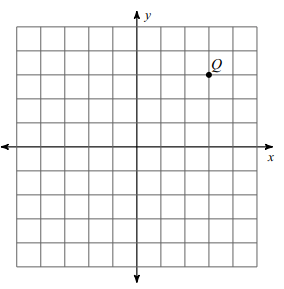
Solution :

Marking the point Q (3, 3). Reflection of Q across y-axis is

Q' (-3, 3)

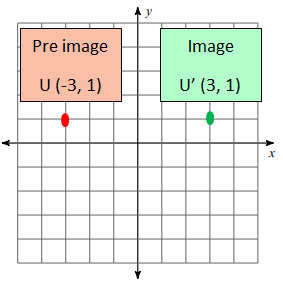
Problem 2 :

Reflection across the x-axis U (-3, 1)

Solution :

Rule :

(x, y) ==> (-x, y)

U (-3, 1) ==> U'(3, 1)

Problem 3 :

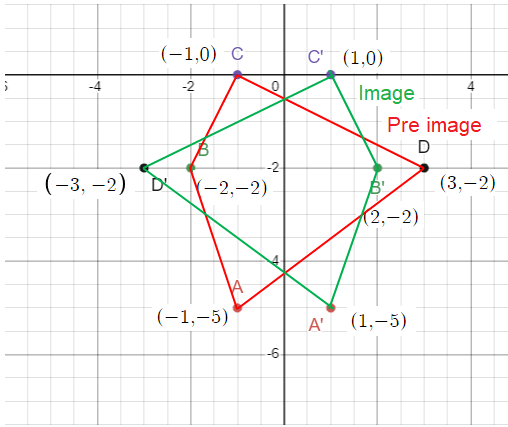
reflection across the y-axis

A (-1, -5), B (-2, -2), C (-1, 0), D (3, -2)

Solution :

Rule : 

(x, y) ==> (-x, y)

A (-1, -5)  ==> A' (1, -5)

B (-2, -2)  ==> B' (2, -2)

C (-1, 0)  ==> C' (1, 0)

D (3, -2)  ==> D' (-3, -2)

Graph the image of the figure using the transformation given.

Problem 4 :

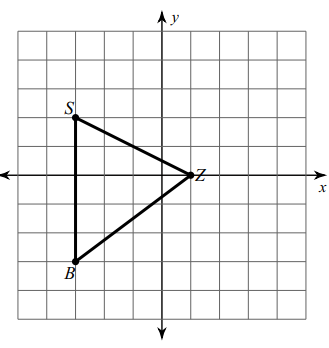
Reflection across the y-axis.

Solution :

By observing the points from the given figure,

S (-3, 2), B (-3, -3) and Z (1, 0)

Rule : 

(x, y) ==> (-x, y)

S (-3, 2)  ==> S' (3, 2)

B (-3, -3) ==> B' (3, -3)

Z (1, 0)  ==> Z' (-1, 0)

Problem 5 :

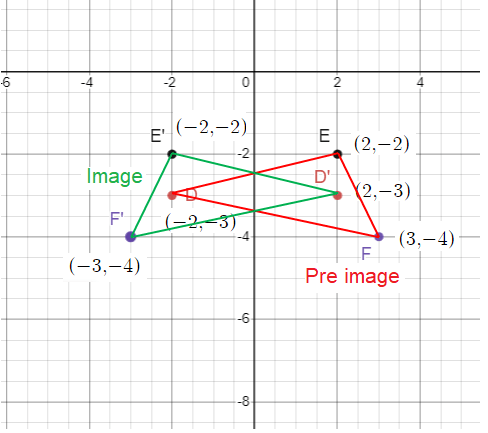
Reflection across the y-axis D(-2, -3), E(2, -2), F(3, -4)

Solution :

Rule : 

(x, y) ==> (-x, y)

D(-2, -3) ==> D' (2, -3)

E(2, -2)  ==> D' (-2, -2)

F(3, -4)  ==> F' (-3, -4)

Find the coordinates of the vertices of each figure after the given transformation.

Problem 6 :

Reflection across the y-axis K(1, −1), N(4, 0), Q(4, −4)

Solution :

Rule : 

(x, y) ==> (-x, y)

K (1, −1) ==> K' (-1, -1)

N (4, 0) ==> N' (-4, 0)

Q (4, −4) ==> Q' (-4, -4)

Problem 7 :

Write a rule to describe each transformation. 

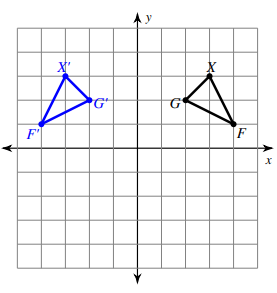
Solution :

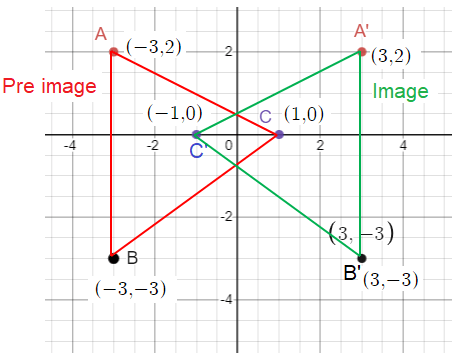
By observing the coordinates of the triangle XGF.

X (3, 3), G (2, 2) and F (4, 1)

Observing the coordinates of the triangle X'G'F'

X' (-3, 3), G' (-2, 2) and F' (-4, 1)

X (3, 3) ==>  X' (-3, 3)

G (2, 2)  ==> G' (-2, 2)

F (4, 1)  ==>  F' (-4, 1)

Clearly the x-coordinate alone changes its sign. So, it is reflection about y-axis.