REFLECTION ACROSS A HORIZONTAL LINE

REFLECTION ABOUT HORIZONTAL LINE

To reflect the image about y = k, we have to draw the horizontal line through k.

Calculate the distance between every vertices on the given shape.

To get the reflected image, we have to go in the opposite direction with the distance.

What is preimage ?

Preimage In a transformation, the original figure is called the preimage.

What is image ?

Image In a transformation, the final figure is called the image.

Graph the image of the figure using the transformation given.

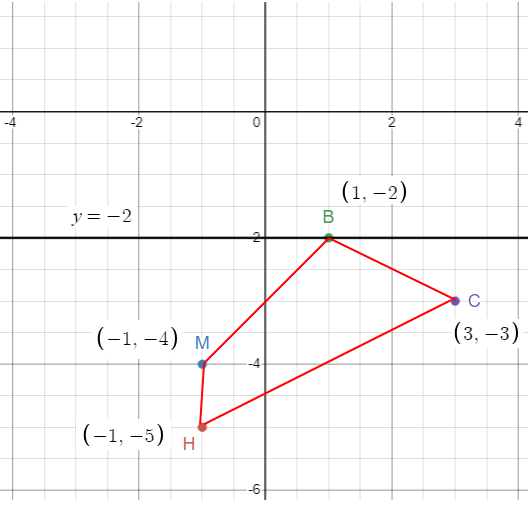
Problem 1 :

Reflection across y = −2

H (−1, −5), M (−1, −4), B (1, −2), C (3, −3)

Solution :

Plotting the points and creating the sides.

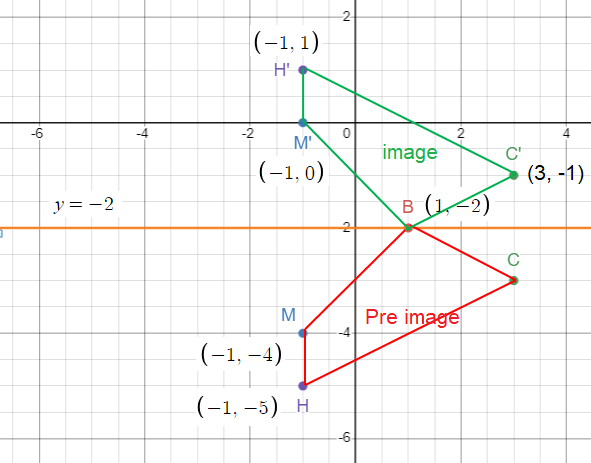
How to get C' ?

To reach the coordinate of C from y = -2, we have to come down 1 unit. So, to get the reflection point of C, that is C' go up 1 unit.

C (3, −3) ==> C' (3, -1)

How to get M' ?

Distance between y = -2 and M is 2 units. Coming down 2 units. To get M' move up 2 units.

M (−1, −4) ==> M' (-1, 0)

How to get H' ?

Distance between y = -2 and H is 3 units. Coming down 3 units. To get H' move up 3 units.

H (−1, −5) ==> H' (-1, 1)

How to get B' ?

Distance between y = -2 and B is 0 units. So, the same point is B'.

B and B are the same.

Problem 2 :

Graph the image of the figure using the transformation given.

 reflection across y = 2

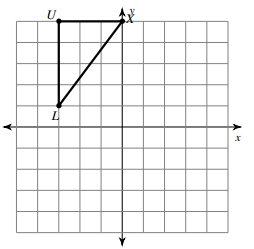
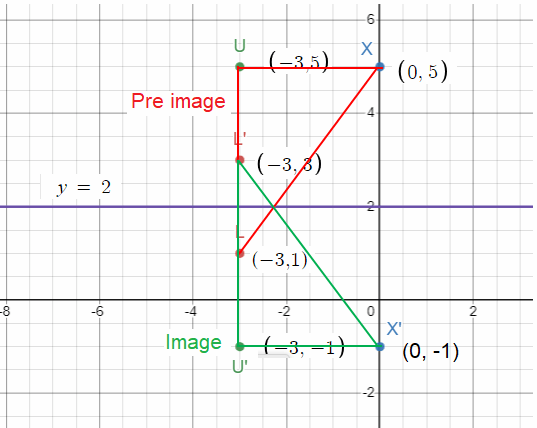
Solution :

By observing the picture, marking the coordinates

L (-3, 1), X (0, 5) and U (-3, 5)

How to get L' ?

To reach L from y = 2, we move down 1 unit. So, to reach the reflection of L, that is L' we have to move up 1 unit.

L (-3, 1) ==> L' (-3, 3)

How to get U' ?

To reach U, we have to move up 3 units from y = 2, so to reach U' move 3 units down.

U (-3, 5) ==>  U' (-3, -1)

How to get X' ?

To reach X, we have to move up 3 units from y = 2, so to reach X' move 3 units down.

 X (0, 5) ==>  X' (0, -1)

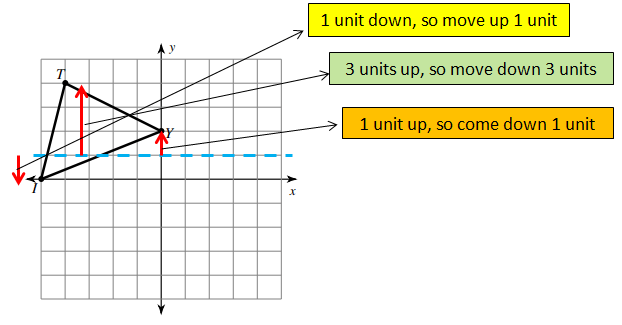
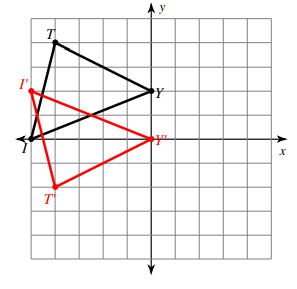
Problem 3 :

Graph the image of the figure using the transformation given

Reflection across y = 1

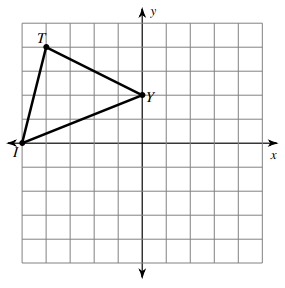
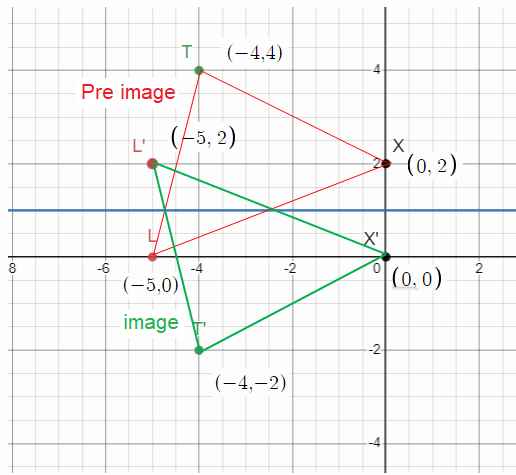
Solution :

By observing the picture, marking the coordinates

L (-5, 0), T (-4, 4) and Y (0, 2)

How to get L' ?

To reach L from y = 1, we move down 1 unit. So, to reach the reflection of L, that is L' we have to move up 1 unit. 

L (-5, 0) ==> L' (-5, 2)

How to get T' ?

To reach T, we have to move up 3 units from y = 1, so to reach T' move 3 units down.

T (-4, 4) ==> T' (-4, -2)

How to get X' ?

To reach X, we have to move up 1 unit from y = 1, so to reach X' move 1 unit down.

X (0, 2) ==> X' (0, 0)

Problem 4 :

Find the coordinates of the vertices of each figure after the given transformation.

Reflection across y = −1

R(−3, −5), N(−4, 0), V(−2, −1), E(0, −4)

Solution :

Reflection of R :

Comparing the y coordinates,

-1 and -5, to reach -5 from -1 we have to move down 4 units. So, to reach R' move up 4 units from y = -1. 

R(−3, −5) ==> R' (-3, 3)

Reflection of N :

Comparing the y coordinates,

-1 and 0, to reach -1 from 0 we have to move up 1 unit. So, to reach N' move down 1 unit from y = -1. 

N(−4, 0) ==> N' (-4, -2)

Reflection of V :

Comparing the y coordinates,

-1 and -1, there is no move

R(−2, -1) ==> R' (-2, -1)

Reflection of E :

Comparing the y coordinates,

-1 and -4, to reach -1 from -4 we have to move down 3 units. So, to reach E' move up 3 units from y = -1. 

E(0, −4) ==> E' (0, 2)