QUESTIONS ON EXTERIOR ANGLES OF A POLYGON

In a convex polygon, the sum of all the exterior angles is equal to 360°. 

One interior angle + Its exterior angle = 180

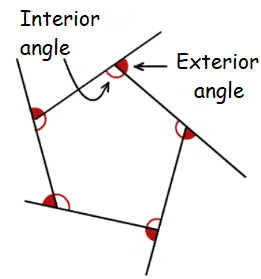
Sum of interior angles of a polygon = 180° × (n-2) 

where n is the number of sides of the polygon

So, the measure of each interior angle of the polygon will be

180° × (n-2) / n 

So, measure of an exterior angle = 180° - 180° × (n-2)/ n

= [180n - 180n + 360]/ n 

= 360/n 

Hence, the sum of all the exterior angles of the polygon is

n × 360/n = 360°

Find, giving reasons, the value of x:

Problem 1 :

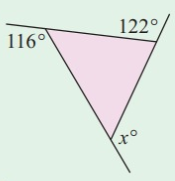
Solution:

The sum of exterior angles of a polygon is 360°.

x° + 116° + 122° = 360°

x° + 238° = 360°

x° = 360 - 238

x° = 122

Problem 2 :

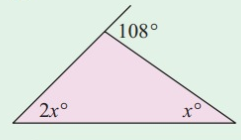
Solution:

2x + x = 108°

3x = 108°

x = 36°

Problem 3 :

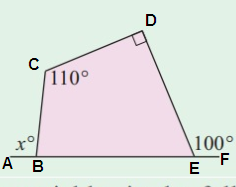
Solution:

∠CDE = 90°

∠CBE + 100° + 90° + 110° = 360°

∠CBE + 300° = 360°

∠CBE = 60°

∠ABC + ∠CBE = 180°

x + 60° = 180°

x = 120°

Problem 4 :

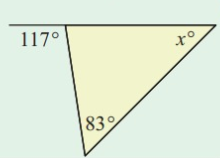
Solution:

83° + x = 117°

x = 117° - 83°

x = 34°

Find the values of the variables in the following diagrams:

Problem 5 :

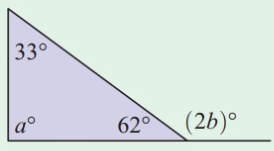
Solution:

a + 33° + 62° = 180°

a + 95° = 180°

a = 180° - 95°

a = 85°

2b = a + 33°

2b = 85° + 33°

2b = 118°

b = 59°

Problem 6 :

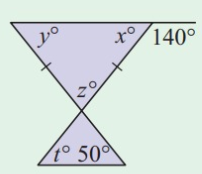
Solution:

x + 140° = 180°

x = 180° - 140°

x = 40°

z + y = 140°

y = 140° - z

y = x

y = 40°

140° - z = 40°

z = 100°

180° = t + 100° + 50°

180° = t + 150°

t = 30°

Problem 7 :

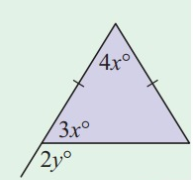
Solution:

Problem 8 :

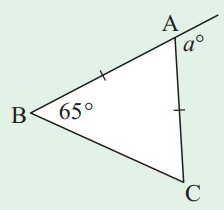
Solution:

a = 65° + 65°

a = 130°

Problem 9 :

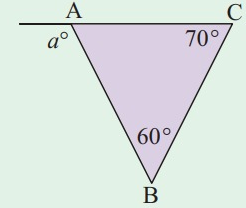
Solution:

70° + 60° = a

a = 130°

Problem 10 :

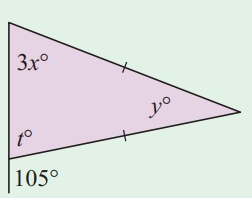
Solution:

t + 105° = 180°

t = 180° - 105°

t = 75°

t = 3x

75° = 3x

x = 25°

3x + y = 105°

3(25) + y = 105°

75 + y = 105°

y = 105° - 75°

y = 30°

Problem 11 :

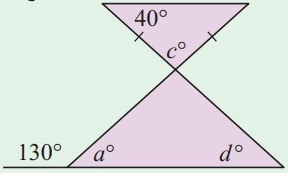
Solution:

a + 130° = 180°

a = 180° - 130°

a = 50°

c + 40° + 40° = 180°

c + 80° = 180°

c = 180° - 80°

c = 100°

Vertically opposite angles will be equal.

The triangle which is at below

a + c + d = 180

50 + 100 + d = 180

d + 150 = 180

d = 180 - 150

d = 30