QUADRATIC FUNCTIONS AND EQUARTIONS PRACTICE TEST FOR SAT

Problem 1 :

The function f is defined by f(x) = x² + bx + c where b and c are constants. If the graph of f has x-intercepts at -5 and 3. Which of the following correctly gives the values of b and c ?

a) b = -5, c = 3      b)  b = -3, c = 5      c)  b = -2, c = - 15

d)  b = 2, c = -15

Solution

Problem 2 :

y = x² - 2x - 3

The parabola in the xy-plane is given by the equation above. Which of the following equivalent forms of the equation displays the coordinate of the vertex of the parabola as constants or coefficients ?

a) y = (x - 1)² - 4            b) y = (x - 1)² - 2

c) y = (x - 3)(x + 1)        d)  y + 3 = x(x + 2)

Solution

Problem 3 :

y = x² + 10x + 16

The equation above represents a parabola in the xy-plane. Which of the following equivalent forms of the equation displays the minimum value of y as a constant or coefficient ?

a) y = (x + 8) (x + 2)       b)  y - 16 = x(x + 10)

c)  y = (x + 5)² - 9        d)  y = (x - 5)² + 9

Solution

Problem 4 :

y = x² - 10x + k

In the equation above, k is constant. If the equation represents a parabola in the xy-plane that is tangent to the x-axis, what is the value of k ?

Solution

Problem 5 :

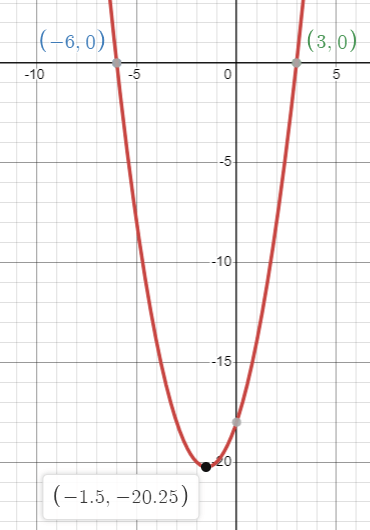
A parabola is shown in the xy-plane above. Which of the following equations correctly represents the parabola by displaying the x-intercepts of the parabola as constants or coefficients ?

a)  y = (x + 1.5)² - 20.25        b)  y = (x - 1.5)² - 20.25

c)  y = (x + 6)(x - 3)           d)  y = (x - 6)(x + 3)

Solution

Problem 6 :

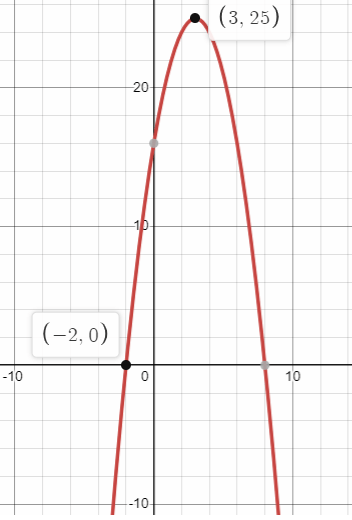
The graph of the equation y = -x² + 6x + 16 is a parabola with (3, 25) as shown in the xy-plane above. If one of the x-intercepts is at -2, which of the following equivalent forms of the equation shows the x-intercepts of the parabola as constant or coefficients ?

a) y = -2(x + 2)(x - 8)      b) y = -(x + 2)(x - 8)

c)  y = (x + 2)(x - 8)        d)  y = -(x - 3)² + 25

Solution

Problem 7 :

In the xy-plane, the graph of a parabola has x-intercepts at -3 and 5. If the y-coordinate of the vertex of the parabola is 8, which of the following could be the equation of parabola ?

Solution

Problem 8 :

h = -6t² + 36t + 12

The height of a model rocket is modeled by the equation above, where h is the height of the rocket, in meters and t is the number of seconds after launch. In which of the following equations the number of seconds it takes the rocket to reach the maximum height appear as constant or coefficients ?

a) h = -6(t +3)² + 42       b)  h = -6(t - 3)² + 66

c)  h = -6(t² - 6t - 2)        d)  h = -6(t - 2)(t - 4) + 60

Solution