QUADRATIC EQUATION PRACTICE PROBLEMS FOR CA FOUNDATION

Problem 1 :

Solving equation x² - (a + b)x + ab = 0, we find the value(s) of x ?

(a)  a      (b)  b   (c) a, b    (d)  None of these

Solution :

Using factoring method, we can decompose ab.

Sum of the factors = a + b and 

Product of factors = ab

x² - (a + b)x + ab = 0

(x - a) (x - b) = 0

Equating each factor to zero, we get

x = a and x = b

Problem 2 :

Solving the equation z + √z = 6/25, then the value of z.

(a)  1/5      (b)  2/5     (c) 1/25      (d)  2/25

Solution :

√z + z = 6/25

Let z = t, then √z = t²

t² - t = 6/25

25t² - 25t - 6 = 0

25t² - 15t - 10t - 6 = 0

5t(5t - 3) - 2(5t - 3) = 0

(5t - 3) (5t - 2) = 0

5t - 3 = 0 and 5t - 2 =0

t = 3/5 and t = 2/5

Problem 3 :

If

(x + 2)/(x - 2) - (x - 2)/(x + 2) = (x - 1)/(x + 3) - (x + 3)/(x - 3)

then the value of x are 

(a)  0, ±√6      (b)   0, ±√3     (c)  0, ±2√3       (d)  None

Solution :

(x + 2)/(x - 2) - (x - 2)/(x + 2) = 

(x - 1)/(x + 3) - (x + 3)/(x - 3)

Simplifying LHS :

(x+2)²-(x-2)²/(x+2) (x-2)

(x+2)² = x² + 4x + 4

(x-2)² = x² - 4x + 4

(x+2)² - (x-2)² = 8x

(x+2) (x-2) = x² - 2² ==>  x² - 4

(x+2)² - (x-2)²/(x+2) (x-2) = 8x/(x² - 4) -----(1)

Simplifying RHS :

(x - 3)/(x + 3) - (x + 3)/(x - 3)

(x-3)² = x² - 6x + 9

(x+3)² = x² + 6x + 9

(x-3)² - (x+3)² = -12x

(x+3) (x-3) = x² - 3² ==>  x² - 9

(x+3)² - (x-3)²/(x+3) (x-3) = -12x/(x² - 9)-----(2)

(1) = (2)

8x/(x² - 4) = -12x/(x² - 9)

2x(x² - 9) = -3x(x² - 4)

2x³ - 18x + 3x³ - 12x = 0

5x³ - 30x = 0

5x(x² - 6) = 0

x = 0 and x = ±√6

Problem 4 :

 Solve (x - 1/x)² + 2(x + 1/x) = 7 1/4

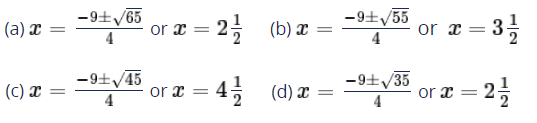
Solution :

Using the algebraic identity

(a - b)² = (a+b)² - 4ab

(x - 1/x)² = (x + 1/x)² - 4x(1/x)

(x - 1/x)² = (x + 1/x)² - 4

By applying this in the given question, we get

(x + 1/x)² - 4 + 2(x + 1/x) = 7 1/4

Let x + 1/x = t

t² + 2t = 29/4 + 4

t² + 2t = 45/4

4t² + 8t = 45

4t² + 8t - 45 = 0

(2t - 5) (2t + 9) = 0

t = 5/2 and t = -9/2

Problem 5 :

The solution of the equation x - √(25 - x²) = 1

(a)  x = -3     (b)  x =  ±5     (c)  x = 1      (d)  x = 4

Solution :

x - √(25 - x²) = 1

√(25 - x²) = x - 1

Taking squares on both sides, we get

(25 - x²) = (x - 1)²

25 - x² = x² - 2x + 1

2x² - 2x - 24 = 0

x² - x - 12 = 0

(x - 4) (x + 3) = 0

x = 4 and x = -3

Problem 6 :

Solve the equation 

(6x + 2)/4 + (2x² - 1)/(2x² + 2) = (10x - 1)/4x we get roots as

(a)  x = -1     (b)  x =  ±1     (c)  x = 1      (d)  x = 0

Solution :

(6x + 2)/4 + (2x² - 1)/(2x² + 2) = (10x - 1)/4x

(3x + 1)/2 + (2x² - 1)/2(x² + 1) = (10x - 1)/4x

(3x + 1) + (2x² - 1)/(x² + 1) = (10x - 1)/2x

2x [(3x + 1)(x² + 1) + (2x² - 1)] = (10x - 1)(x² + 1)

2x [3x³ + 3x + x² + 1 + 2x² - 1] = 10x³ + 10x - x² - 1

2x [3x³ + 3x² + 3x] = 10x³ + 10x - x² - 1

6x⁴ + 6x³ + 6x² - 10x³ - 10x + x² + 1 = 0

6x⁴ - 4x³ + 7x² - 10x + 1 = 0

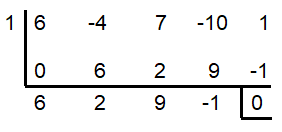
So, x = 1 is one of the solution.

Problem 7 :

If α and β  are the roots of

x² = x + 1

then the value of α²/β - β²/α is

(a)  2√5      (b)  √5     (c)  3√5      (d)  -2√5

Solution :

x² = x + 1

x² - x - 1 = 0

Sum of the roots (α + β) = 1

Product of the roots (αβ) = -1

α²/β - β²/α = (α³ - β³)/αβ --------(1)

(α³ - β³) = (α - β)³ + 3αβ(α - β)

(α - β) = √(α + β)²-4(α β)

(α - β) = √5

(α³ - β³) = (√5)³ + 3(-1)(√5)

(α³ - β³) = 5√5 - 3√5

(α³ - β³) = 2√5

By applying the value in (1), we get

α²/β - β²/α = 2√5/(-1)

= -2√5

Problem 8 :

Solving x² + y² - 25 = 0 and x - y - 1 = 0, we get the roots 

(a)  ±3, ±4     (b)  ±2, ±3     (c)  0, 3,  4      (d)  0, -3, -4

Solution :

From x - y - 1 = 0, we get x = y + 1

By applying the value of x in x² + y² - 25 = 0, we get

(y + 1)² + y² - 25 = 0

y² + 2y + 1 + y² - 25 = 0

2y² + 2y - 24 = 0

y² + y - 12 = 0

(y + 4) (y - 3) = 0

y = -4 and y = 3

So, the answer is option (a).

Problem 9 :

The roots of a ax² + bx + c = 0, are real and unequal if

(a) b²< 4ac     (b) b² = 4ac   (c) b² > 4ac    (d) None

Solution :

If the roots are real and unequal, then 

b² -  4ac > 0

b² > 4ac

Problem 10 :

α, β are the roots of the equation x² - 5x + 6 = 0 the equation with the roots (α β + α + β) and (α β - α - β) is 

(a) x² - 12x + 11 = 0    (b) 2x² - 6x + 12 = 0

(c) x² - 12x - 12 = 0    (d) None

Solution :

Sum of the roots = α β + α + β + α β - α - β

= 2 α β

Product of roots = (α β + α + β) (α β - α - β)

= (α β + α + β) (α β - (α + β))

= (α β)² - (α + β)²

From the equation, x² - 5x + 6 = 0

α + β = 5 and αβ = 6

Applying these values in sum and product of roots, we get

Sum of the roots = 12

and

Product of the roots = 6² - 5²

= 36 - 25

= 11

Quadratic equation having the roots α and β will be in the form

x² - (Sum of roots) x + Product of roots = 0

x² - 12x + 11 = 0 

Problem 11 :

If p ≠ q and p² = 5p - 3 and q² = 5q - 3 the equation having roots as p/q and q/p is

(a) x² - 19x + 3 = 0    (b) 3x² - 19x - 3 = 0

(c) 3x² - 19x + 3 = 0    (d) 3x² + 19x + 3 = 0

Solution :

 p/q and q/p are the roots

Sum of roots = 5/1 ==> 5 (α + β)

Product of roots = 3/1 ==> 3 (α β)

Sum of roots =  (p/q) + (q/p)

= (p² + q²) /pq

= [(p + q)² - 2pq] /pq

= [52 - 2(3)]/3

= 19/3

Product of roots = (p/q)  (q/p) = 1

So, the required equation is 

x² - (19/3)x + 1 = 0

3x² - 19x + 3 = 0