PROPORTIONAL RELATIONSHIP

Problem 1 :

Determine if each of the following equations represents a proportional or nonproportional relationship.

(i)  d = 65t

(ii)  p = 0.1s + 2000

(iii)  n = 450 − 3p

(iv)  36 = 12d

A linear relationship is a proportional relationship when y/x is constant. Otherwise, the linear relationship is nonproportional.

Solution :

(i)  d = 65t

Since the given equation is in the form of y = kx, it is a proportional relationship.

Constant of proportionality = 65.

(ii)  p = 0.1s + 2000

0.1s is added by 2000. So, it is not in proportional relationship.

(iii)  n = 450 − 3p

By rewriting as, n = -3p + 450

-3p is added by 450. It is not a proportional relationship.

(iv)  36 = 12d

There is no relationship between two variables. So, there is no proportional relationship.

From the Table

Problem 2 :

Determine if the linear relationship represented by each table is a proportional or nonproportional relationship.

(i)

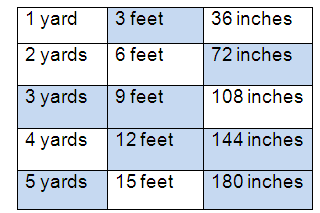
Solution :

When x = 2, y = 30

Constant of proportionality (k) = y/x

k = 30/2 ==>  15

When x = 8, y = 90

k = 90/8 ==>  45/4

Since constant of proportionality are not equal, it is not in proportional relationship.

(ii)

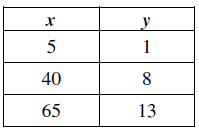
Solution :

When x = 5, y = 1

Constant of proportionality (k) = y/x

k = 1/5

When x = 40, y = 8

k = 8/40 ==>  1/5

Since constant of proportionality are equal, it is in proportional relationship.

From the Statement

Problem 3 :

Determine which situation is a proportional relationship and which situation is a nonproportional relationship.

(i)  The cost for Test Prep Center A is $20 times the number of hours that you attend. 

Solution :

Let C be the cost for test preparation center A.

h be the number of hours.

C = 20h

It is a proportional relationship.

(ii)  The cost for Test Prep Center B is $25 an hour, but you have a $100 coupon that you can use to reduce the cost.

Solution :

C = 100 - 25h

It is non proportional relationship.

From the Graph

Problem 4 :

Determine if each relationship is a proportional or nonproportional situation.

(i)

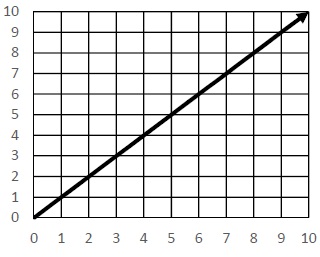
Solution :

Since the line passes through the origin, it is a proportional relationship.

(ii)

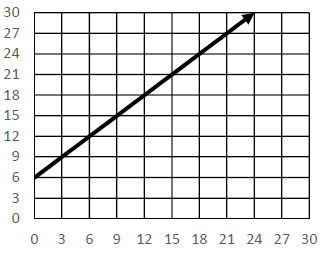
Solution :

Since the line does not passes through the origin, it is a non proportional relationship.