PROPORTIONAL PARTS AND SCALE FACTOR

Problem 1 :

Some special effects in movie are created using miniature models. In a recent movie, a model sports utility (SUV) 22 inches long was created to look like a real 14  2/3 foot SUV. What is the scale factor of the model compared to the real SUV ?

Solution :

Converting foot to inches :

1 foot = 12 inches

14  2/3 foot = 14  2/3 x 12 inches

= (44/3) x 12

= 176 inches

Scale factor = Length of miniature / length of original

= 22/176

= 1/8

So, the model is 1/8 of the real.

Problem 2 :

The two polygons are similar, write similarity statement and find x, y and UT.

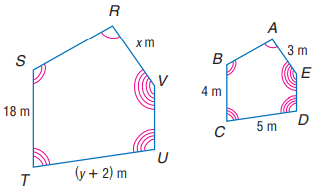
Solution :

From the given information polygons RVUTS and ABCDE are similar.

RV and AE are corresponding sides. ST and BC are corresponding sides.

ST/BC = 18/4 ==> 9/2

The two polygons are in the ratio 9 : 2

RV/AE = x/3 ---(1)

Equating (1) to scale factor,

x/3 = 9/2

x = 13.5

TU/CD = (y + 2)/5 ---(2)

Equating (2) to scale factor

(y + 2)/5 = 9/2

2(y + 2) = 9(5)

2y + 4 = 45

2y = 45 - 4

2y = 41

y = 41/2

y = 20.5

UT = y + 2

UT = 20.5 + 2 ==> 22.5

Problem 3 :

Each pair of polygons is similar. Write a similarity statement, find x and measures of indicated sides and scale factor.

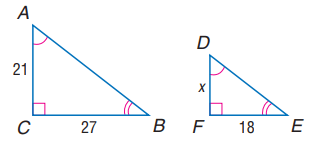
Solution :

BC/EF = 27/18 ---(1)

AC/DF = 21/x ---(2)

(1) = (2)

27/18 = 21/x

27x = 21(18)

x = 14

Scale factor :

BC/EF = 27/18

BC/EF = 3/2

So, the required scale factor is 3 : 2.

Problem 4 :

Each pair of polygons is similar. Write a similarity statement, find x and measures of indicated sides and scale factor. Find the lengths of FE, EH and GF.

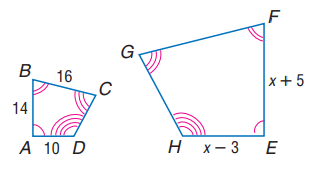
Solution :

AD/HE = AB/EF

10/(x - 3) = 14/(x + 5)

10(x + 5) = 14(x - 3)

10x + 50 = 14x - 42

10x - 14x = -42 - 50

-4x = -92

x = 23

FE = x + 5 ==> 28

EH = x - 3 ==> 20

AD/HE = 10/20 ==> 1/2

So, the scale factor is 1/2.

BC = 1/2 of GF

16 = (GF/2)

GF = 32

Each pair of polygons is similar. Write a similarity statement, find x and measures of indicated sides and scale factor.

Problem 5 :

 Find the lengths of AB and CD.

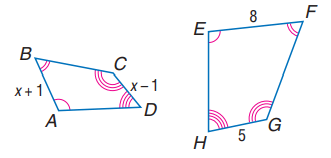
Solution :

DC/HG = AB/EF

(x - 1)/5 = (x + 1)/8

8(x - 1) = 5(x + 1)

8x - 8 = 5x + 5

8x - 5x = 5 + 8

3x = 13

x = 13/3

Problem 6 :

Find AC and CE.

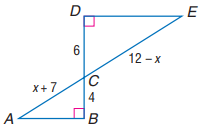
Solution :

∠ACB =  ∠DCE

∠CBA =  ∠CDE

The triangles ACB and DCE are similar.

AC/EC = BC/DC

(x + 7) / (12 - x) = 4/6

6(x + 7) = 4(12 - x)

6x + 42 = 48 - 4x

6x + 4x = 48 - 42

10x = 6

x = 6/10

x = 0.6

AC = 0.6 + 7 => 7.6

CE = 12 - 0.6 => 11.4

Problem 7 :

Find BC and ED.

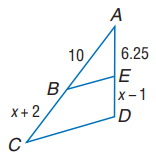
Solution :

The triangles ABE and ACD are similar.

AB/AC = AE/AD

10/(x + 2 + 10) = 6.25/(x - 1 + 6.25)

10/(x + 12) = 6.25/(x + 5.25)

10(x + 5.25) = 6.25(x + 12)

10x + 52.5 = 6.25x + 75

10x - 6.25x = 75 - 52.5

3.75x = 22.5

x = 6

AC/EC = BC/DC

(x + 7) / (12 - x) = 4/6

6(x + 7) = 4(12 - x)

6x + 42 = 48 - 4x

6x + 4x = 48 - 42

10x = 6

x = 6/10

x = 0.6

AC = 0.6 + 7 => 7.6

CE = 12 - 0.6 => 11.4