PROPERTIES OF TRIANGLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A triangle is a polygon which has three sides.
All triangles have the following properties.
- The sum of the interior angles of a triangle is 180°
- Any exterior angle is equal to sum of the interior opposite angles.
- The longest side is opposite to the largest angle.
- The triangle is the only rigid polygon.
- The sum of any two sides of a triangle is greater than or equal to the third side.
Find the values of the variables, give brief reasons.
Problem 1 :
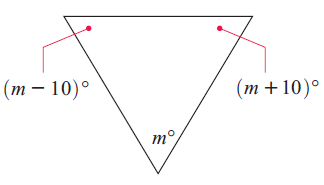
Solution :
Property :
Sum of the interior angles = 180
m - 10 + m + m + 10 = 180
3m = 180
Divide by 3 on both sides.
m = 180/3
m = 60
Problem 2 :
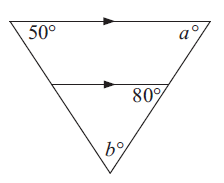
Solution :
Property :
One of the sides of the triangle and the line passes through the other two sides are parallel, corresponding angles are equal.
a = 80
Sum of interior angles of a triangle = 180
50 + b + a = 180
50 + b + 80 = 180
130 + b= 180
b = 180 - 150
b = 30
Problem 3 :
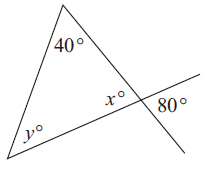
Solution :
Property :
At the point of intersection, vertically opposite angles are equal.
x = 80
y + 40 + x = 180
y + 40 + 80 = 180
y + 120 = 180
Subtracting 120 on both sides.
y = 180 - 120
y = 60
Problem 4 :
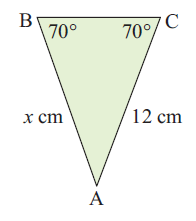
Solution :
Property :
In any isosceles triangle, two of the angles will be equal. The sides which is opposite to the equal angle measure will be equal in length.
Since ∠B = ∠C
x = 12 cm
Problem 5 :
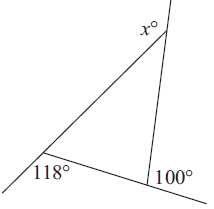
Solution :
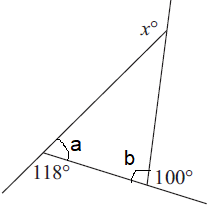
|
118 + a = 180 a = 180 - 118 a = 62 |
b + 100 = 180 a = 180 - 100 a = 80 |
Property :
Using exterior angle theorem.
x = a + b
x = 62 + 80
x = 142
Problem 6 :
Triangle TAB has a perimeter of 40 cm. Could the measures of the sides, as shown, actually represent the measures of the sides of a triangle?
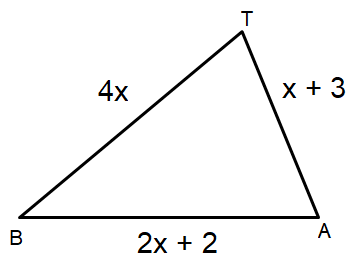
Solution :
Perimeter of the triangle TAB = 40 cm
4x + x + 3 + 2x + 2 = 40
7x + 5 = 40
Subtracting 5 on both sides.
7x = 40 - 5
7x = 35
Dividing by 7 on both sides.
x = 35/7
x = 5
|
BA = 2x + 2 BA = 2(5) + 2 AB = 12 |
AT = x + 3 AT = 5 + 3 AT = 8 |
BT = 4x BT = 4(5) BT = 20 |
So, the sides of the triangle are 12, 8 and 20
Using triangle inequality theorem :
12 + 8 > 20
8 + 20 > 12
12 + 20 > 8
So, these measures will not be the sides of the triangle.
Problem 7 :
Two sides of an isosceles triangle measure 4 and 8. Which of the following choices could be the measure of the third side?
(a) 10 (b) 8 (c) 6 (d) 4
Solution :
Let the sides of the triangle be a, b and c.
If a = 4, b = 8, then c = 4 or 8.
Case 1 :
Let a = 4, b = 8 and c = 4
4 + 8 > 4 (True)
4 + 4 > 8 (Not true)
Since these sides are not satisfying triangle inequality theorem, it will not be sides of the triangle.
Case 2 :
Let a = 4, b = 8 and c = 8
4 + 8 > 8 (True)
8 + 8 > 4 (True)
Since these sides are satisfying the triangle inequality theorem, it will be sides of the triangle.
So, the third side must be 8.
Problem 8 :
In ΔGAB, m∠G = 35º and m∠A = 52º. Which side of the triangle is the longest side?
Solution :
In triangle, the angles measures are m∠G, m∠A, m∠B.
m∠G + m∠A + m∠B = 180
35 + 52 + m∠B = 180
84 + m∠B = 180
Subtracting 84 on both sides.
m∠B = 180 - 84
m∠B = 96
Since the largest angle measure is m∠B, then the side which is opposite to this angle measure will be the longest side.
The longest side is AG.
Problem 9 :
In ΔABC, AB = 4x + 2, BC = 5x - 3, and AC = 2x + 4. The perimeter of the triangle is 36 units. Which angle in the triangle has the largest measure?
Solution :
Perimeter of the triangle ABC = 36
AB = 4x + 2, BC = 5x - 3, and AC = 2x + 4.
4x + 2 + 5x - 3 + 2x + 4 = 36
11x + 2 - 3 + 4 = 36
11x + 3 = 36
Subtracting 3 on both sides.
11x = 36 - 3
11x = 33
Dividing by 11 on both sides.
x = 33/11
x = 3
|
AB = 4x + 2 = 4(3) + 2 = 12 + 2 = 14 |
BC = 5x - 3 = 5(3) - 3 = 15 - 3 = 12 |
AC = 2x + 4 = 2(3) + 4 = 6 + 4 = 10 |
So, the largest measure is 14, that is AB. Angle C is the greatest measure.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling