PROPERTIES OF PARALLELOGRAM

Parallelogram

Definition of parallelogram :

A parallelogram is a quadrilateral which has opposite sides parallel.

Properties of parallelogram :

• Opposite sides are equal in length
• Opposite angles are equal in size.
• Diagonals bisect each other.
• Consecutive interior angles add upto 180.

Problem 1 :

Find each measure in parallelogram

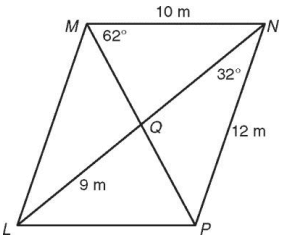
Find, 

1)  ML    2)  LP   3)  ∠LPM   4)  ∠MLN    5)  LN    6)  QN

Solution :

Since it is parallelogram, the opposite sides are parallel and equal ML = PN and LP = MN

1)  ML = 12 m

2)  LP = 10 m

3)  MN and LP are parallel, MP is a transversal. 

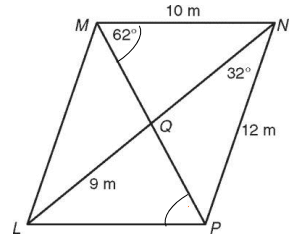
∠PMN = ∠LPM = 62° (Alternate interior angles)

4)  ∠MLN

LM parallel to PN, then 

∠MLN = ∠LNP = 32° (Alternate interior angles)

5)  LN :

Since the diagonal will bisect each other, LP = NQ

LN = 2LP

LN = 2(9) ==> 18

6)  QN = 9 m

Problem 2 :

CDEF is a parallelogram. Find each measure.

(i)  CD   (ii)  EF     (iii)  ∠E     (iv)  ∠F

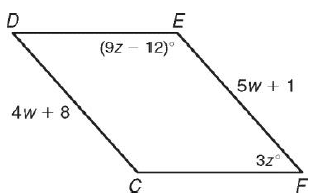
Solution :

In parallelogram opposite sides will be equal.

CD = EF

Sum of consecutive interior angles = 180.

9z - 12 + 3z = 180

12z - 12 = 180

12z = 192

z = 192/12

z = 16

Problem 3 :

Quadrilateral RSTU is a parallelogram. Find the values of x, y, a, and b.

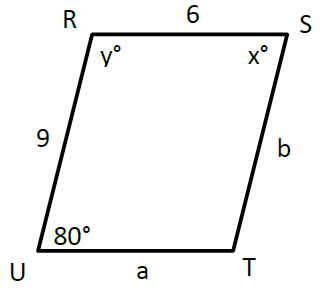
Solution :

x = 80° 

x + y = 180 (Consecutive interior angles)

80 + y = 180

y = 180 - 80

y = 100

a = 6 and b = 9

Problem 4 :

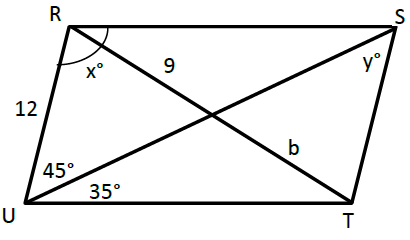
Solution :

In triangle RUS.

∠URS + ∠RSU + ∠SUR = 180

∠RSU = 35 (Alternate interior angles)

x + 35 + 45 = 180

x + 80 = 180

x = 180 - 80

x = 100

y = 45 (Alternate interior)

Diagonal will bisect each other. So, b = 9.

Problem 5 :

Find the missing measurements of parallelogram.

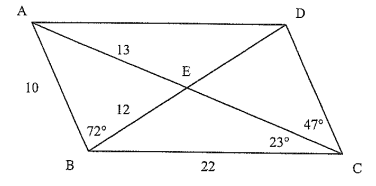
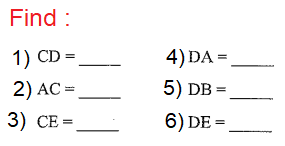
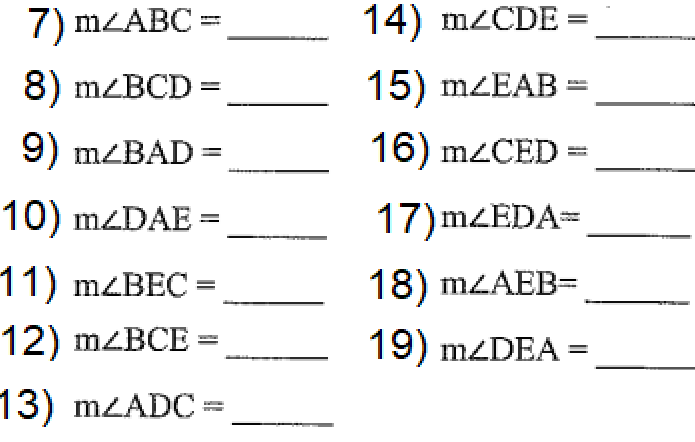
Solution :

1) CD = 10 (Opposite sides)

2)  AC = 13 + 13 ==> 26

3)  CE = 13

4)  DA = 22 (Opposite sides)

5)  DB = 12 + 12 ==> 24

6)  DE = 12

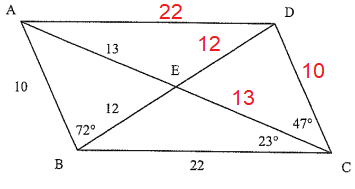
7)  In triangle ABC,

∠EBC = x

∠EAB + ∠ABE + ∠EBC + ∠BCE = 180

47 + 72 + x + 23 = 180

142 + x = 180

x = 180 - 142

x = 38

∠ABC = 72 + 38 ==>  110

8) ∠BCD = 23 + 47 ==>  70

9) ∠BAD = 23 + 47 ==>  70

10) ∠DAE = 23

11) ∠BEC :

In triangle BEC,

38 + 23 + ∠BEC = 180

∠BEC = 180 - 61

∠BEC = 119

12)  ∠BCE = 23

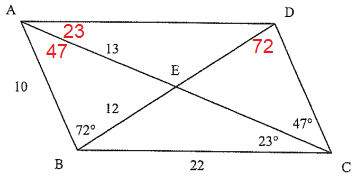
13) ∠ADC :

∠ABC = ∠ADC  =  110 (opposite angles)

14)  ∠CDE = 72 (Alternate angles)

15)  ∠EAB = 47

16)  ∠CED :

∠CED = 180 - (47 + 72)

∠CED = 180 - 119

∠CED = 61

17)  ∠EDA = 38 (alternate interior angles)

18)  ∠AEB = 61

19)  ∠DEA = 119

Problem 8 :

In the figure given below, ABCD is a parallelogram. Find the values of x, y, z and p.

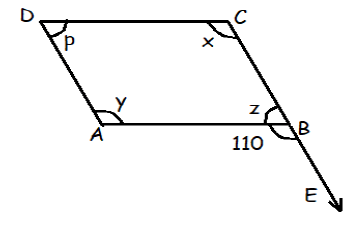
Solution :

110 + z = 180

z = 180 - 110

z = 70

In parallelogram sum of consecutive angles = 180

y + z = 180

y + 70 = 180

y = 110

Opposite angles are equal,

So, x = 110 and p = 70

Related Pages

• Find missing angles in parallelogram
• Find missing angles of parallelogram worksheet
• Length of diagonal of parallelogram
• Length of diagonal of parallelogram worksheet
• Properties of parallelogram worksheet