PROPERTIES OF INTERSECTING CHORDS INSIDE A CIRCLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
If two chords intersect inside a circle, then the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord.
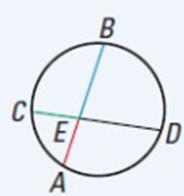
EA ∙ EB = EC ∙ ED
Problem 1 :
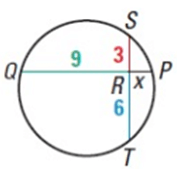
Find the value of x.
Solution :
Notice that ST and QP are chords that intersect at R.
RS ∙ RT = RQ ∙ RP
3 ∙ 6 = 9 ∙ x
18 = 9x
x = 2
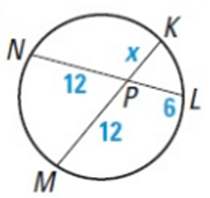
Find the value of x.
Problem 1:
Solution :
PK ∙ PM = PL ∙ PN
x ∙ 12 = 6 ∙ 12
12x = 72
x = 6
Problem 2 :
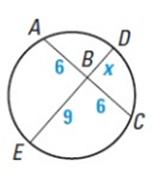
Solution :
BA ∙ BC = BD ∙ BE
6 ∙ 6 = x ∙ 9
36 = 9x
x = 4
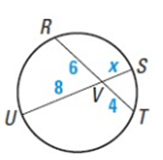
Problem 3 :
Solution :
VR ∙ VT = VS ∙ VU
6 ∙ 4 = x ∙ 8
24 = 8x
x = 3
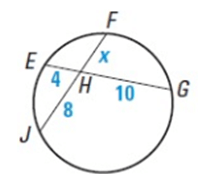
Problem 4 :
Solution :
HE ∙ HG = HF ∙ HJ
4 ∙ 10 = x ∙ 8
40 = 8x
x = 5
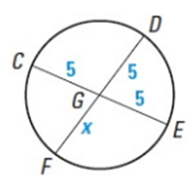
Problem 5 :
Solution :
GC ∙ GE = GD ∙ GF
5 ∙ 5 = 5 ∙ X
25 = 5x
x = 5
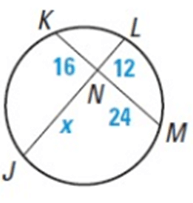
Problem 6:
Solution :
NJ ∙ NL = NK ∙ NM
x ∙ 12 = 16 ∙ 24
12x = 384
x = 32
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling