PROPERTIES OF A RECTANGLE WITH DIAGONALS AND ANGLES

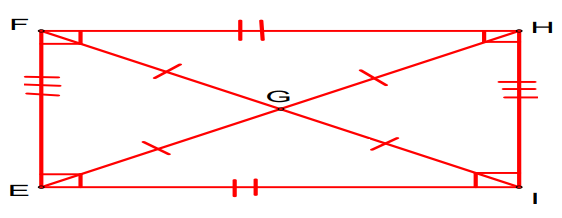
• Length of opposite sides will be equal.
• Length of diagonals will be equal.
• Diagonal will bisect each other in the point where it meets each other.
• All corner angles will be right angles.
• Diagonals are not angle bisector of corner angles.

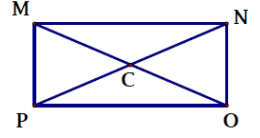
MNOP is a rectangle, with diagonals that intersect at C. Find the value of each variable or the missing part.

Problem 1 :

If MO = 4x - 60 and MC = x + 5

Solution :

In the rectangle given above, MO and PN are diagonals. Diagonals of rectangle are congruent and it will bisect at the point of intersection.

MO = 2 MC

4x - 60 = 2(x + 5)

4x - 60 = 2x + 10

4x - 2x = 10 + 60

2x = 70

x = 70/2

x = 35

Problem 2 :

Find ∠CMP

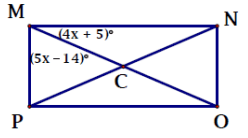
Solution :

∠PMC + ∠CMN = 90

5x - 14 + 4x + 5 = 90

9x - 9 = 90

9x = 90 + 9

9x = 99

x = 99/9

x = 11

∠CMP = 5 x - 14

= 5(11) - 14

= 55 - 14

= 41

Problem 3 :

Use the information marked on the figure to find the value of x.

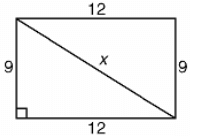
Solution :

Using Pythagorean theorem,

x² = 9² + 12²

x² = 81 + 144

x² = 225

x = 15

Problem 4 :

In rectangle ABCD, diagonals AC and BD intersect at point E. If AE = 20 and BD = 2x + 30, find x.

Solution :

Here AC and BD are diagonals.

AC = 2 AE

BD = 2AE

2x + 30 = 2(20)

2x + 30 = 40

2x = 40 - 30

2x = 10

x = 10/2

x = 5

Problem 5 :

In rectangle MATH, MT = 2x +12 and AH = 3x +2. What is the value of MT?

Solution :

AH and MT are diagonals.

3x + 2 = 2x + 12

3x - 2x = 12 - 2

x = 10

MT = 2x + 12

Applying the value if x, we get

MT = 2(10) + 12

= 20 + 12

MT = 32

Problem 6 :

A rectangular garage, 27 feet by 36 feet, is being built. To ensure a right angle where the sides meet, what should each diagonal measure?

Solution :

Diagonal of the rectangular shape will be the hypotenuse of the triangle.

(Hypotenuse)² = Sum of square of remaining two sides.

(Hypotenuse)² = 27² + 36²

(Hypotenuse)² = 729 + 1296

(Hypotenuse)² = 2025

Hypotenuse = √2025

Hypotenuse = 45

MNOP is a rectangle, with diagonals that intersect at C. Find the value of each variable or the missing part.

Problem 7 :

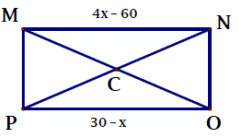
Solution :

In rectangle, length of opposite sides will be equal.

PO = MN

30 - x = 4x - 60

-x - 4x = -60 - 30

-5x = -90

x = 90/5

x = 18

Problem 8 :

MO = 4x - 60 and MC = x + 5

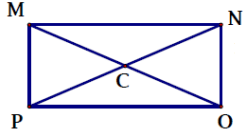
Solution :

MO is the diagonal of the rectangle. MC is the bisector of the diagonal. So,

MO = 2 MC

4x - 60 = 2(x + 5)

4x - 60 = 2x + 10

4x - 2x = 10 + 60

2x = 70

x = 70/2

x = 35

Problem 9 :

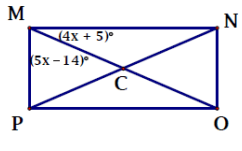
Solution :

Each corner angle measure is 90 degree.

∠PMC + ∠CMN = 90

5x - 14 + 4x + 5 = 90

9x - 9 = 90

9x = 90 + 9

9x = 99

x = 99/9

x = 11

Problem 10 :

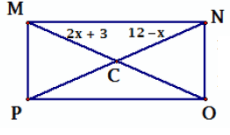
Solution :

MO and PN are diagonals. Diagonals will bisect each other at the point C.

MC = NC 

2x + 3 = 12 - x

2x +x = 12 - 3

3x = 9

x = 9/3

x = 3

Problem 11 :

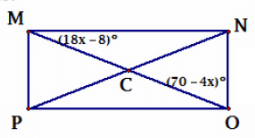
Solution :

Sum of interior angles in a triangle = 180

 ∠NMO +  ∠NOM +  ∠MNO = 180

18x - 8 + 70 - 4x + 90 = 180

14x + 62 = 180 - 90

14x + 62 = 90

14x = 90 - 62

14x = 28

x = 28/14

x = 2