PRODUCT RULE OF EXPONENTS

Product Rule of Exponents :

When multiplying exponential expressions that have the same base, add the exponents.

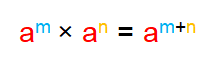
Simplify each of the following.

Example 1 :

a ⋅ a² ⋅ a³

Solution :

Using product rule a^m × aⁿ = a^m+n

= a ⋅ a² ⋅ a³

= a¹⁺² ⋅ a³

= a³ ⋅ a³

= a³⁺³

= a⁶

Example 2 :

(2a²b)(4ab²)

Solution :

= (2a²b)(4ab²)

Multiply the coefficients,

= (2 × 4) (a²b) (ab²)

= 8(a²b) (ab²)

Combining like terms,

= 8(a² ⋅ a) (b ⋅ b²)

By  a^m × aⁿ = a^m+n, we get

= 8(a²⁺¹) (b¹⁺²)

= 8a³b³

Example 3 :

(6x²)(-3x⁵)

Solution :

= (6x²)(-3x⁵)

Multiply the coefficients,

= (6 × (-3)) (x²) (x⁵)

By  a^m × aⁿ = a^m+n, we get

= -18(x²⁺⁵)

= -18x⁷

Example 4 :

b³ ⋅ b⁴ ⋅ b⁷⋅ b

Solution :

= b³ ⋅ b⁴ ⋅ b⁷⋅ b

= b^{3 + 4 + 7 + 1}

= b¹⁵

Example 5 :

(3x³) (3x⁴) (-3x²)

Solution :

= (3x³) (3x⁴) (-3x²)

While multiplying monomials, we have to follow the order

i) multiplying the signs

ii) multiplying the coefficients

iii) multiplying the variables

= 3 × 3 × (-3) (x³) (x⁴) (x²)

= -27 (x^{3 + 4 + 2}) 

= -27 x⁹ 

Use the product rule to rewrite each expression as a single exponent.

Example 6 :

(-5)^-10 ⋅ (-5)¹⁵

Solution :

= (-5)^-10 ⋅ (-5)¹⁵

= (-5)^-10+15

= (-5)⁵

= 1/(-5)⁵

= -1/5⁵

Example 7 :

Solution :

Example 8 :

(1.4)^-12 ⋅ (1.4)⁵

Solution :

= (1.4)^-12 ⋅ (1.4)⁵

= (1.4)^-12+5

= (1.4)^-7

By changing the negative exponent to positive exponent, we get

= 1/(1.4)⁷

Example 9 :

Solution :

Example 10 :

(-13)⁰ ⋅ (-13)^-19

Solution :

= (-13)⁰ ⋅ (-13)^-19

= 1⋅ (-13)^-19

=  1/(-13)¹⁹

=  -1/13¹⁹

Example 11 :

8^-14 ⋅ 8⁴

Solution :

= 8^-14 ⋅ 8⁴

= 8^-14+4

= 8^-10

By changing the negative exponent to positive exponent, we get

= 1/8¹⁰

Find the value of x :

Example 12 :

10^x ⋅ 10^-9 = 10¹¹

Solution :

10^x ⋅ 10^-9 = 10¹¹

10^x-9 = 10¹¹

Since bases are the same, equate the powers.

x - 9 = 11

x = 11 + 9

x = 20

Example 13 :

Solution :

Example 14 :

(-2.9)^-13 ⋅ (-2.9)^x = (-2.9)^-5

Solution :

(-2.9)^-13 ⋅ (-2.9)^x = (-2.9)^-5

(-2.9)^-13+x = (-2.9)^-5

Since bases are the same, equate the powers.

-13 + x = -5

x = -5 + 13

x = 8

Example 15 :

The human body has about 100 billion cells. This number can be written in exponential form as

(a) 10^–11      (b) 10¹¹     (c) 10⁹    (d) 10^–9

Solution :

1 billion = 1,000,000,000

1 billion cosist of nine zeroes

100 billion = 100000000000

100 billion consists of eleven zeroes, then writing it in exponential form we get

= 10¹¹

Option b is correct.

Example 16 :

(-2)³ ⋅ (-2)⁷ / (3 ⋅ 4⁶)

Solution :

= (-2)³ ⋅ (-2)⁷ / (3 ⋅ 4⁶)

= (-2)³⁺⁷ / (3 ⋅ ((2)²)⁶)

= (-2)¹⁰ / (3 ⋅ 2¹²)

= 2¹⁰ / (3 ⋅ 2¹²)

= 1 / (3 ⋅ 2²)

= 1/12

Example 17 :

The value of (–2)^{2×3 –1} is

(a) 32     (b) 64    (c) – 32     (d) – 64

Solution :

= (–2)^{2×3 –1}

= (–2)^{6 - 1}

= (–2)⁵

= –2⁵

= -32

Example 18 :

(2^-1+ 4^–1 + 6^–1 + 8^–1)^x = 1

Solution :

(1/2 + 1/4 + 1/6 + 1/8)^x = 1

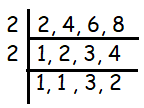
2 x 2 x 3 x 2

LCM (2, 4, 6 and 8) = 24

(1/2 + 1/4 + 1/6 + 1/8)^x = 1

((12 + 6 + 4 + 3)/24)^x = 1

(25/24)^x = 1

(25/24)^x = (25/24)⁰

x = 0

Example 19 :

Find the value of x^–3 if x = (100)^{1 - 4} ÷ (100)⁰

Solution :

x = (100)^{1 - 4} ÷ (100)⁰

x = (100)^-3 ÷ 1

x = 1/100³

x = 1/(10²)³

x = 1/10⁶

x^-3 = (1/10⁶)^-3

x^-3 = (1/10⁶)^-3

x^-3 = (10⁶)³

x^-3 = 10¹⁸

Example 20 :

By what number should we multiply (–29)⁰ so that the product becomes (+29)⁰.

Solution :

The value of (–29)⁰ is 1. Because anything raised by the power 0 is 1.

(–29)⁰ should be multiplied by 1, so we will recieve (+29)⁰.

Example 21 :

By what number should (–15)^–1 be divided so that quotient may be equal to (–15)^–1?

Solution :

By observing the question and answer, we recieve the same answer. Any number divided by 1 will recieive the same number as result.

So, the required number is 1.

Example 22 :

Find the multiplicative inverse of (–7)^–2 ÷ (90)^–1

Solution :

= (–7)^–2 ÷ (90)^–1

= (90)¹ ÷(–7)²

= 90/49

Multiplicative inverse of 90/49 is 49/90

Example 23 :

If 5^3x–1 ÷ 25 = 125, find the value of x.

Solution :

5^3x–1 ÷ 25 = 125

5^3x–1 ÷ 5² = 5³

5^{3x – 1- 2} = 5³

5^{3x – 3} = 5³

3x - 3 = 3

3x = 3 + 3

3x = 6

x = 6/3

x = 2