PROBLEMS USING PROPERTIES OF KITE

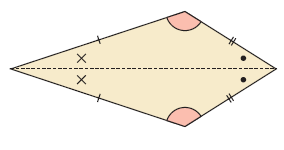
Definition of kite :

A kite is a quadrilateral which has two pairs of adjacent sides equal in length.

Properties :

• One diagonal is an axis of symmetry.
• One pair of opposite angles are equal.
• Diagonals cut each other at right angles.
• One diagonal bisect one pair of angles at vertices.

Find the measures of the numbered angles in each kite.

Problem 1 :

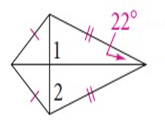
Solution :

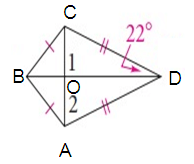
∠1 = ∠COD = 90^º

∠2 = ∠DAO

∠CDO = 22^º  = ∠ADO

In a triangle DAO,

∠DOA + ∠DAO + ∠CDO = 180^º

90^º + ∠DAO + 22^º = 180º

112^º + ∠DAO = 180^º

∠DAO = 180^º - 112^º

∠DAO = 68^º

Problem 2 :

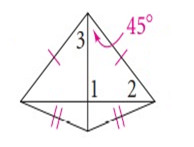
Solution :

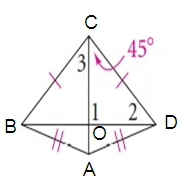
∠1 = ∠COD = 90^º

∠2 = ∠ODC

∠3 = ∠OCD = 45^º

In a triangle COD,

∠COD + ∠ODC + ∠OCD = 180^º

90^º + ∠ODC + 45^º = 180º

135^º + ∠ODC = 180^º

∠ODC = 180^º - 135^º

∠ODC = 45^º

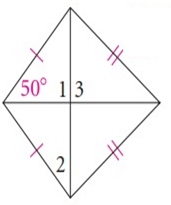
Problem 3 :

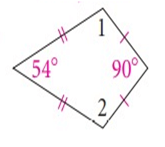
Solution :

The pair of m < A and m < C must be congruent.

That is,

m ∠A ≈ m ∠C

Let, m ∠A = m ∠C = x^º

We know that the four angles of a quadrilateral add up to 360^º.

So, we have

m ∠A + m ∠B + m ∠C + m ∠D = 360^º

x^º + 54^º + x^º + 90^º = 360^º

2x^º + 144^º = 360^º

Subtract 144^º from both sides.

2x^º + 144^º - 144^º = 360^º – 144^º

2x^º = 216^º

Divide both sides by 2.

2x^º/2 = 216^º/2

x^º = 108^º

Hence, we have

m ∠A = m ∠C = 108^º

Problem 4 :

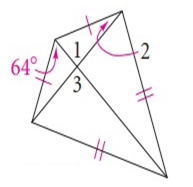
Solution :

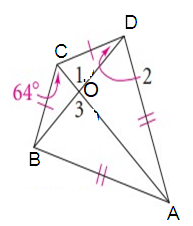
∠1 = ∠3

∠COD = ∠AOB = 90^º

∠2 = ∠CDO

∠OCB = 64^º = ∠OCB

In a triangle OCD,

∠COD + ∠OCB + ∠CDO = 180^º

90^º + 64^º + ∠CDO = 180º

154^º + ∠CDO = 180^º

∠CDO = 180^º - 154^º

∠CDO = 26^º

Problem 5 :

Solution :

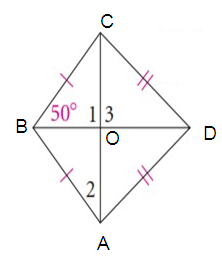
∠1 = ∠3

∠COB = ∠COD = 90^º

∠2 = ∠OAB

∠CBO = 50^º = ∠OBA

In a triangle OAB,

∠BOA + ∠OAB + ∠OBA = 180^º

90^º + ∠OAB + 50^º = 180º

140^º + ∠OAB = 180^º

∠OAB = 180^º - 140^º

∠OAB = 40^º

Problem 6 :

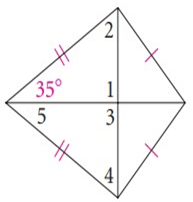
Solution :

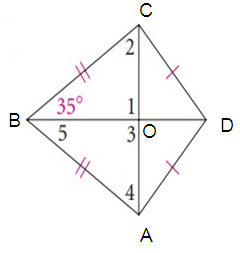
∠1 = ∠3

∠COB = ∠AOB = 90^º

∠2 = ∠OCB

∠4 = ∠OAB

∠5 = ∠OBA

∠CBO = 35^º

In a triangle COB,

∠COB + ∠OCB + ∠CBO = 180^º

90^º + ∠OCB + 35^º = 180º

125^º + ∠OCB = 180^º

∠OCB = 180^º - 125^º

∠2 = ∠OCB = 55^º

In a triangle OAB,

∠COB + ∠OAB + ∠CBO = 180^º

90^º + ∠OAB + 35^º = 180º

125^º + ∠OAB = 180^º

∠OAB = 180^º - 125^º

∠4 = ∠OAB = 55^º

In a triangle OCB,

∠COB + ∠OAB + ∠OBA = 180^º

90^º + ∠55^º + ∠OBA = 180º

145^º + ∠OBA = 180^º

∠OBA = 180^º - 145^º

∠5 = ∠OBA = 35^º

Problem 7 :

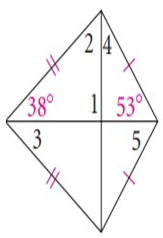
Solution :

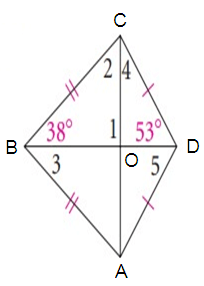
∠1 = ∠COB = 90^º

∠2 = ∠OCB

∠3 = <OBA = ∠CBO = 38^º

∠4 = ∠OCD

∠5 = ∠ADO = ∠CDO = 53^º

In a triangle COB,

∠COB + ∠OCB + ∠CBO = 180^º

90^º + ∠OCB + 38^º = 180^º

128^º + ∠OCB= 180^º

∠OCB = 180^º - 128^º

∠OCB = 52^º

In a triangle,

∠OCD + ∠CDO + ∠COB = 180^º

∠OCD + 53^º + 90^º = 180^º

143^º + ∠OCD= 180^º

∠OCD = 180^º - 143^º

∠OCD = 37^º

Problem 8 :

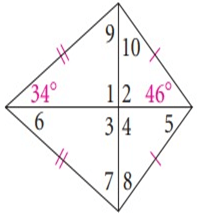
Solution :

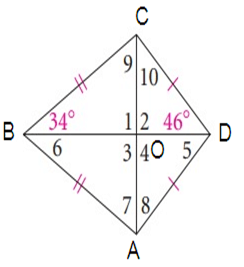
∠1 = ∠2 = ∠3 = ∠4

∠COB = ∠COD = ∠AOB = ∠AOD = 90^º

∠5 = ODA = ∠CDO = 46^º

∠6 = OBA = ∠OBC = 34^º

∠7 = ∠OAB

∠8 = ∠OAD

∠9 = ∠OCB

∠10 = ∠OCD

In a triangle AOB,

∠AOB + ∠OAB + ∠OBA = 180^º

 90^º + ∠OAB + 34^º= 180^º

124^º + ∠OAB= 180^º

∠OAB = 180^º - 124^º

∠OAB = 56^º

In a triangle AOD,

∠OAD + ∠AOD + ∠ODA = 180^º

∠OAD + 90^º + 46^º= 180^º

∠OAD + 136^º= 180^º

∠OAD = 180^º - 136^º

∠OAD = 44^º

In a triangle OCB,

∠OCB + ∠COB + ∠OBA = 180^º

∠OCB + 90^º + 34^º= 180^º

∠OCB + 124^º= 180^º

∠OCB = 180^º - 124^º

∠OCB = 56^º

In a triangle OCD,

∠OCD + ∠COD + ∠CDO = 180^º

∠OCD + 90^º + 46^º= 180^º

∠OCD + 136^º= 180^º

∠OCD = 180^º - 136^º

∠OCD = 44^º

Problem 9 :

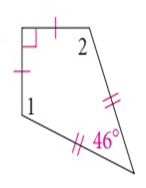
Solution :

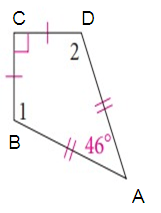
The pair of m ∠A and m ∠C must be congruent.

That is,

m ∠A ≈ m ∠C

Let, m ∠A = m ∠C = x^º

m ∠A + m ∠B + m ∠C + m ∠D = 360^º

46^º + x^º + 90^º + x^º = 360^º

2x^º + 136^º = 360^º

Subtract 136^º from both sides.

2x^º + 136^º - 136^º = 360^º – 136^º

2x^º = 224^º

Divide both sides by 2.

2x^º/2 = 224^º/2

x^º = 112^º

Hence, we have

m ∠A = m ∠C = 112^º

Problem 10 :

Given WXYZ is a kite, m∠YWX = 2x + 30, and m∠WYX = 4x. Find m∠YWX.

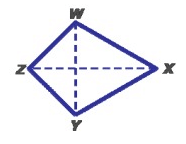
Solution :

By observing the figure,

2x + 30 = 4x

Subtract 2x from both sides.

2x – 2x + 30 = 4x – 2x

30 = 2x

Divide both sides by 2.

30/2 = 2x/2

15 = x

So, the value is x = 15.