PROBLEMS USING SOACAHTOA

Find the value of the trigonometric ratio. Express answers as a fraction in lowest terms.

Problem 1 :

Find sin x.

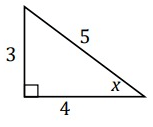
Solution :

sin x = opposite/hypotenuse

= AB/AC

= 3/5

So, sin x = 3/5.

Problem 2 :

Find cos x.

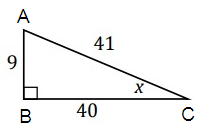
Solution :

cos x = adjacent/hypotenuse

= BC/AC

= 40/41

So, cos x = 40/41.

Problem 3 :

Find tan x

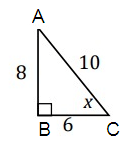
Solution :

tan x = opposite/adjacent

= AB/BC

= 8/6

= 4/3

So, tan x = 4/3.

Problem 4 :

Find cos x.

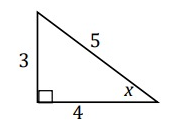
Solution :

cos x = adjacent/hypotenuse

= BC/AC

= 4/5

So, cos x = 4/5.

Problem 5 :

Find sin x.

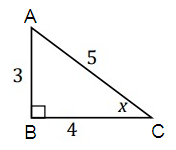
Solution :

sin x = opposite/hypotenuse

= AB/AC

= 9/41

So, sin x = 9/41.

Problem 6 :

Find sin x

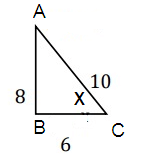
Solution :

sin x = opposite/hypotenuse

= 8/10

= 4/5

So, sin x = 4/5.

Problem 7 :

Find tan x.

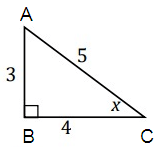
Solution :

tan x = opposite/adjacent

= AB/BC

= 3/4

So, tan x = 3/4.

Problem 8 :

Find tan x.

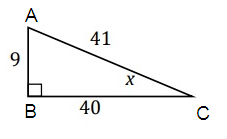
Solution :

tan x = opposite/adjacent

= AB/BC

= 9/40

So, tan x = 9/40.

Problem 9 :

Fins cos x.

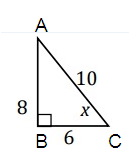
Solution :

cos x = adjacent/hypotenuse

= BC/AC

= 6/10

So, cos x = 3/5.

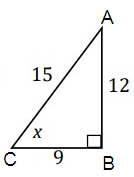
Problem 10 :

Find tan x.

Solution :

tan x = opposite/adjacent

= AB/BC

= 12/9

So, tan x = 4/3.

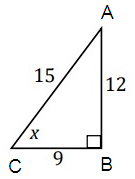
Problem 11 :

Find cos x.

Solution :

cos x = adjacent/hypotenuse

= BC/AC

= 9/15

= 3/5

So, cos x = 3/5.

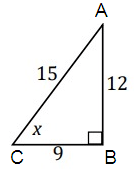
Problem 12 :

Find sin x

Solution :

sin x = opposite/hypotenuse

= AB/AC

= 12/15

= 4/5

So, sin x = 4/5.