CHECKING TYPES OF DISCONTINUITY
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
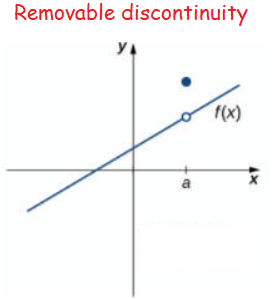
Removable Discontinuity:
Removable discontinuities occur when a rational function has a factor with an x that exists in both the numerator and the denominator. Removable discontinuities are shown in a graph by a hollow circle that is also known as a hole. Below is the graph for
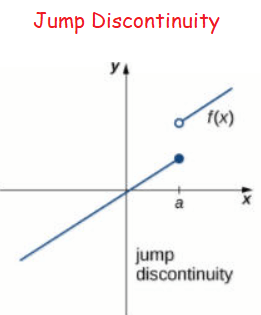
Jump discontinuity :
The function's curve would be labeled as discontinuous as it jumps from one point to another at the function's discontinuity point.
In short, the function approaches different values depending on which direction X is moving.
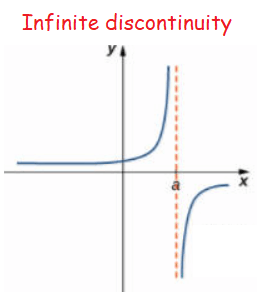
Non removable of infinite discontinuity :
An infinite discontinuity occurs when a function has a vertical asymptote on one or both sides. This is shown in the graph of the function below at x = a.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
State whether or not each of the following functions is continuous.
- If not, state where the discontinuity occurs and whether or not it is removable.
- Is the discontinuity is an asymptote, a hole or jump ?
- If an asymptote, what is its equation ?
Problem 1 :
Solution :
For any real values of x, the function will not become undefined. So, it is continuous for all real values.
Problem 2 :
Solution :
Equating the denominators to zero, we get
|
2x + 1 = 0 2x = -1 x = -1/2 |
x - 1 = 0 x = 1 |
The function is discontinuous at x = -1/2 and 1.
Type of discontinuity = Non removable
Vertical asymptotes are at x = -1/2 and x = 1.
Problem 3 :
Solution :
Equating the denominators to 0, we get
|
x - 3 = 0 x = 3 |
x + 2 = 0 x = -2 |
The function is discontinuous at x = 3 and -2.
Type of discontinuity = Non removable
Vertical asymptotes are at x = 3 and x = -2.
Problem 4 :
Solution :
It is not continuous at x = 4 and x = -4. Removing the common factor, we get f(x) = 1/(x + 4)
Equating the denominator to 0, we get
x + 4 = 0
x = -4
So, the vertical asymptote is at x = -4
Hole is at x = 4. When x = 4, y = 1/5
Problem 5 :
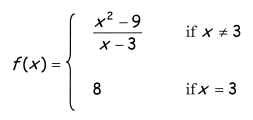
Solution :
The function is not continuous at x = 3, there is removable discontinuity at (3, 6).
Problem 6 :
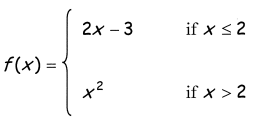
Solution :
Lim x->2- f(x) = Lim x->2- 2x - 3
Applying the limit, we get
Lim x->2- f(x) = 2(2) - 3
= 4 - 3
= 1
Lim x->2+ f(x) = Lim x->2+ x2
Applying the limit, we get
Lim x->2+ f(x) = 22
= 4
Since Lim x->2- f(x) = Lim x->2+ f(x), then lim x ->2 f(x) does not exists.
Type of discontinuity = Jump discontinuity
Problem 7 :
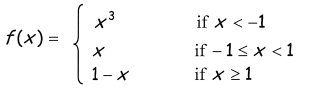
Solution :
Lim x->-1- f(x) = Lim x->-1- x3
Applying the limit, we get
Lim x->-1- f(x) = (-1)3
= -1 -----(1)
Lim x->-1+ f(x) = Lim x->-1+ x
Applying the limit, we get
Lim x->-1+ f(x) = -1-----(2)
(1) = (2)
At x = -1, the function is continuous.
Lim x->1- f(x) = Lim x->1- x
Applying the limit, we get
Lim x->1- f(x) = 1 -----(1)
Lim x->1+ f(x) = Lim x->1+ (1 - x)
Applying the limit, we get
Lim x->1+ f(x) = 1 - 1
= 0 ----(2)
(1) ≠ (2)
At x = 1, the function is not continuous, then the limit does not exists.
There is jump discontinuity at x = 1.
Problem 8 :
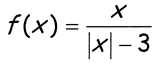
Solution :
|x| - 3
When x is positive
x - 3
When x is negative
-x - 3
f(x) is not continuous at x = 3 and x = -3, there is vertical asymptote at x = 3 and x = -3
Problem 9 :
Find the value of a if the function is continuous.
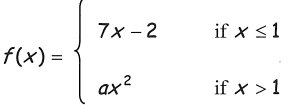
Solution :
Lim x->1- f(x) = Lim x->1- 7x - 2
Applying the limit, we get
Lim x->1- f(x) = 7(1) - 2
= 5 ----(1)
Lim x->1+ f(x) = Lim x->1+ ax2
Applying the limit, we get
Lim x->1+ f(x) = a(1)2
= a----(2)
(1) = (2)
a = 5
Problem 10 :
Find the value of a if the function is continuous.
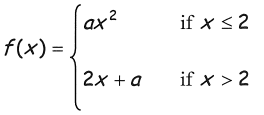
Solution :
Lim x->2- f(x) = Lim x->2- ax2
Applying the limit, we get
Lim x->2- f(x) = a(2)2
= 4a ----(1)
Lim x->2+ f(x) = Lim x->2+ 2x + a
Applying the limit, we get
Lim x->2+ f(x) = 2(2) + a
= 4 + a----(2)
(1) = (2)
4a = 4 + a
4a - a = 4
3a = 4
a = 4/3
Problem 11 :
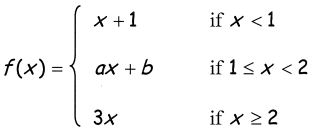
Solution :
lim x->1- f(x) = Lim x->1- x + 1
Applying the limit, we get
Lim x->1- f(x) = 1 + 1
= 2
Lim x->1+ f(x) = Lim x->1+ ax + b
Applying the limit, we get
Lim x->1+ f(x) = a(1) + b
= a + b
Equating left hand limit and right hand limit, we get
a + b = 2 ----(1)
lim x->2- f(x) = Lim x->2- ax + b
Applying the limit, we get
Lim x->2- f(x) = a(2) + b
= 2a + b
Lim x->2+ f(x) = Lim x->2+ 3x
Applying the limit, we get
Lim x->2+ f(x) = 3(2)
= 6
Equating the left hand limit and right hand limit, we get
2a + b = 6 ----(2)
(1) - (2)
a + b - (2a + b) = 2 - 6
-a = -4
a = 4
Applying the value of a in (1), we get
2(4) + b = 6
b = 6 - 8
b = -2
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling