PROBLEMS ON TRIGONOMETRY AND INVERSE TRIGONOMETRIC FUNCTIONS

Find the exact value of the expression.

Problem 1 :

Solution :

Then θ lies in second quadrant.

Problem 2 :

Solution :

Find the exact value of the expression.

Problem 3 :

Solution :

Then θ lies in first quadrant.

Problem 4 :

Find the exact value of the expression.

Solution :

Problem 5 :

Use a right triangle to write the expression as an algebraic expression. Assume that x is positive and in the domain of the given inverse trigonometric function.

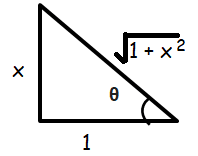
sin (tan^-1 x)

Solution :

Given, sin (tan^-1 x)

Let tan^-1 x = θ

x = tan θ

Problem 6 :

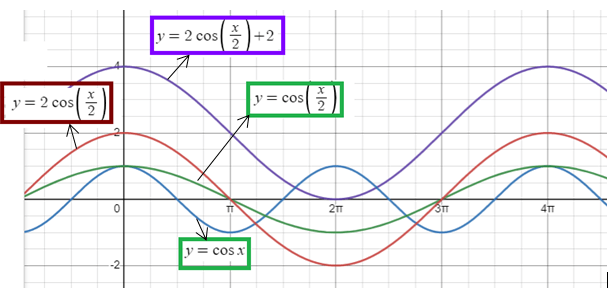
Use a transformations to graph the function.

y = 2 cos (1/2) x + 2

Solution :

Problem 7 :

Use the given information to find the exact value of the expression.

sin θ  = 15/17, θ lies in quadrant I

Find cos 2θ.

Solution :

sin θ  = 15/17

cos 2θ =1 - 2 sin²θ

Problem 8 :

Find all solutions of the equation.

2 cos x - 1 = 0

Solution :

2 cos x - 1 = 0

2 cos x = 1

cos x = 1/2

x = cos^-1 1/2

x = π/3

Therefore we have that the solutions to our equations are as follows.

 x = π/3 + 2nπ (n is a integer) and (2π is a radians)

Problem 9 :

Solve the equation on the interval [0, 2π]

cos x + 2 cos x sin x = 0

Solution :

Given, cos x + 2 cos x sin x = 0

cos x (1+ 2 sin x) = 0

cos x = 0

x = (2n + 1)π/2

n is any integer. (0, 1, ...)

x = π/2 or 3π/2

1 + 2 sinx = 0

2 sinx = -1

sin x = -1/2

x = (π + π/6)

π = 1

x = 7π/6 

Problem 10 :

Solve the equation on the interval [0, 2π]

2 cos²x + sin x - 2 = 0

Solution :

2 cos²x + sin x - 2 = 0

2(1 - sin² x) + sin x - 2 = 0

2 - 2sin² x + sin x - 2 = 0

-2 sin² x + sin x = 0

sin x[-2 sin x + 1] = 0

sin x = 0

-2 sin x + 1 = 0

-2 sin x = -1

sin x = 1/2

sin x = 0 when x = 0, π, 2π

sin x = 1/2 when x = π/6, 5π/6.