PROBLEMS ON TRANSLATION OF 2D SHAPES

Graph the image of the figure using the transformation given.

Problem 1 :

Translate the shape 2 units right and 1 unit up.

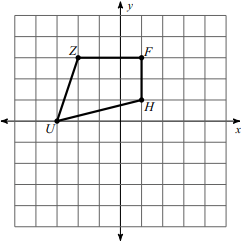
Solution :

Writing the vertices,

U (-3, 0), Z (-2, 3), F (1, 3) and H (1, 1)

We translate the figure 2 units right and 1 unit up. So, 

(x, y) ===> (x + 2, y + 1)

U (-3, 0) ==> U' (-3+2, 0+1) ==> U' (-1, 1)

Z (-2, 3) ==> Z' (-2+2, 3+1) ==> Z' (0, 4)

F (1, 3) ==> Z' (1+2, 3+1) ==> F' (3, 4)

H (1, 1) ==> H' (1+2, 1+1) ==> Z' (3, 2)

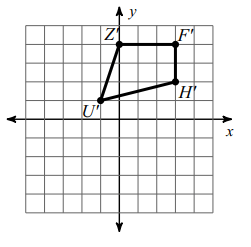
Problem 2 :

Translate the shape 2 units left and 3 units up.

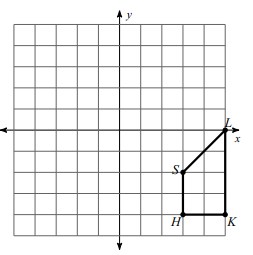
Solution :

Writing the vertices,

S (3, -2), L (5, 0), H (3, -4) and K (5, -4)

We translate the figure 2 units left and 3 units up. So,

(x, y) ===> (x - 2, y + 3)

S (3, -2) ==> S' (-3-2, -2+3) ==> S' (-5, 1)

L (5, 0) ==> L' (5-2, 0+3) ==> L' (3, 3)

H (3, -4) ==> H' (3-2, -4+3) ==> H' (1, -1)

K (5, -4) ==> K' (5-2, -4+3) ==> K' (3, -1)

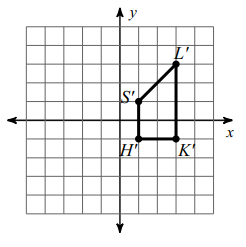
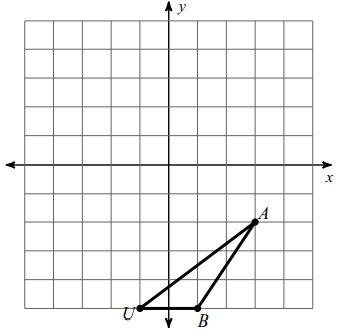
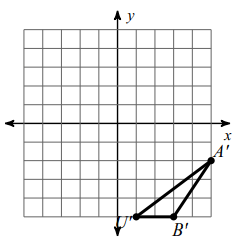
Problem 3 :

Translate the shape 2 units right.

Solution :

Writing the vertices,

A (3, -2), U (-1, -5), B (1, -5)

We translate the figure 2 units right. So,

(x, y) ===> (x + 2, y)

A (3, -2) ==> A' (3+2, -2) ==> A' (5, -2)

U (-1, -5) ==> U' (-1+2, -5) ==> U' (1, -5)

B (1, -5) ==> B' (1+2, -5) ==> B' (3, -5)

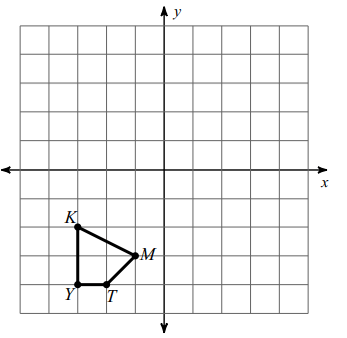
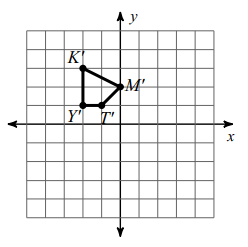
Problem 4 :

Translate the shape 1 unit right and 5 units up.

Solution :

Writing the vertices,

K (-3, -2), Y (-3, -4), T (-2, -4) and M (-1, -3)

We translate the figure 1 unit right and 5 units up.. So,

(x, y) ===> (x + 1, y + 5)

K (-3, -2) ==> K' (-3+1, -2+5) ==> K' (-2, 3)

Y (-3, -4) ==> Y' (-3+1, -4+5) ==> Y' (-2, 1)

T (-2, -4) ==> T' (-2+1, -4+5) ==> T' (-1, 1)

M (-1, -3) ==> M' (-1+1, -3+5) ==> M' (0, 2)

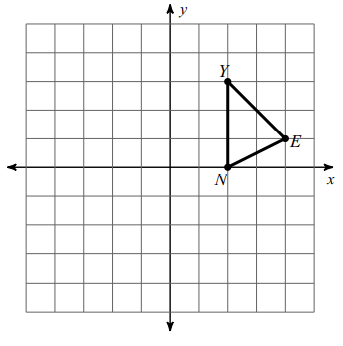
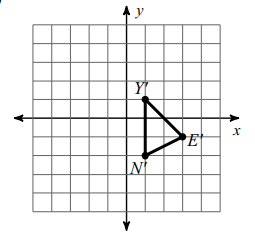
Problem 5 :

Translate the shape 1 unit left and 2 units down.

Solution :

Writing the vertices,

N (2, 0), E(-4, 1), Y (2, 3)

We translate the figure 1 unit left and 2 units down. So,

(x, y) ===> (x - 1, y - 2)

N (2, 0) ==> N' (-2-1, 0-2) ==> N' (-3, -2)

E (-4,1)  ==> Y' (-4-1, 1-2) ==> E' (-5, -1)

Y (2, 3) ==> Y' (2-1, 3-2) ==> Y' (1, 1)

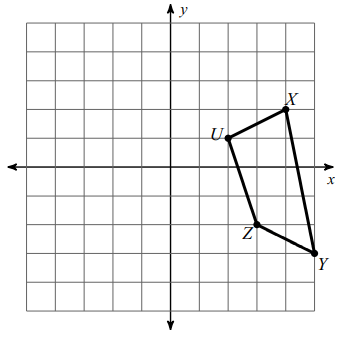
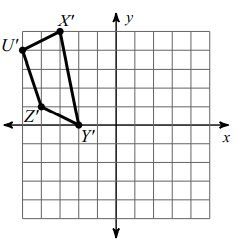
Problem 6 :

Translate the shape 7 units left and 3 units up.

Solution :

Writing the vertices,

Z (3, -2), U(2, 1), X (4, 2) and Y(5, -3)

We translate the figure 7 units left and 3 units up. So,

(x, y) ===> (x - 7, y + 3)

Z (3, -2) ==> Z' (3-7, -2+3) ==> Z' (-4, 1)

U (2,1)  ==> U' (2-7, 1+3) ==> U' (-5, 4)

X (4, 2) ==> X' (4-7, 2+3) ==> X' (-3, 5)

Y (5, -3) ==> Y' (5-7, -3+3) ==> Y' (-2, 0)