PROBLEMS ON REMAINDER THEOREM WITH UNKNOWN VALUE

Problem 1 :

Given that x − 2 is a factor of the polynomial

x³ − kx² − 24x + 28

find k and the roots of this polynomial.

Solution :

x - 2 is a factor, then x = 2 is a zero.

Let p(x) = x³ − kx² − 24x + 28

p(2) =  2³ − k(2)² − 24(2) + 28

0 = 8 - 4k - 48 + 28

0 = 36 - 48 - 4k

0 = -12 - 4k

-4k = 12

k = -3

Applying the value of k, we get x³ + 3x² − 24x + 28

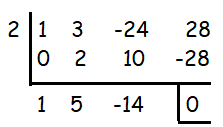
The quotient = x² + 5x - 14

By factoring this quotient, we will get the factors.

(x + 7) (x - 2)

So, the factors are (x + 7)(x - 2) and (x - 2).

Problem 2 :

Find the quadratic whose roots are −1 and 1/3 nd whose value at x = 2 is 10.

Solution :

Roots are x = -1 and x = 1/3

So, the factors are (x + 1) and (x - 1/3)

p(x) be the required polynomial.

p(x) = a(x + 1) (x - 1/3)

p(2) = a(2+1)(2-1/3)

10 = a(3)(5/3)

a = 10/5

a = 2

By applying the value of a in p(x), we get

So, the required quadratic polynomial is

p(x) = 2(x + 1) (x - 1/3)

Problem 3 :

Consider the polynomial p(x) = x³ − 4x² + ax − 3.

(a) Find a if, when p(x) is divided by x + 1, the remainder is −12.

(b) Find all the factors of p(x).

Solution :

x + 1 = 0

x = -1

p(-1) = (-1)³ − 4(-1)² + a(-1) − 3

0 = -1 - 4 - a - 3

0 = -8 - a

a = -8

By applying the value of a in the polynomial p(x), we get

p(x) = x³ − 4x² - 8x − 3

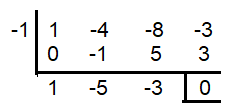
(x + 1) and (x² - 5x - 3) are factors.

Problem 4 :

Consider the polynomial

h(x) = 3x³ − kx² − 6x + 8

(a) Given that x − 4 is a factor of h(x), find k and find the other factors of h(x).

Solution :

x - 4 is a factor, then x = 4 is a zero.

h(4) = 3(4)³ − k(4)² − 6(4) + 8

0 = 3(64) − 16k − 24 + 8

0 = 192 - 16k - 16

0 = 176 - 16k

16k = 176

k = 11

Problem 5 :

Find the quadratic which has a remainder of −6 when divided by x − 1, a remainder of −4 when divided by x − 3 and no remainder when divided by x + 1

Solution :

Let p(x) = k (x - a) (x - b) the required quadratic polynomial.

p(x) = k (x - a) (x - b) ----(1)

When p(x) is divided by x - 1, the remainder will be -6

x - 1 = 0

x = 1 an p(1) = -6

Applying the value x = 1 in (1), we get

p(1) = k(1 - a)(1 - b)

-6 = k(1 - a) (1 - b) ---(2)

When p(x) is divided by x - 3, the remainder will be -4

x - 3 = 0

x = 3 an p(3) = -4

Applying the value x = 3 in (1), we get

p(3) = k(3 - a)(3 - b)

-4 = k(3 - a) (3 - b) ---(3)

No remainder, that is p(-1) = 0

p(-1) = k(-1 - a)(-1 - b)

0 = k(-1 - a)(-1 - b)

(-1-a) (-1-b) = 0

-1-a = 0

a = -1

Applying the value of a in (2), we get

-6 = k(1+1) (1 - b)

-3 = k(1 - b)

k = -3/(1 - b)

Applying the value of a in (3), we get

-4 = k(3 + 1) (3 - b)

-1 = k(3 - b)

k = -1/(3 - b)

Equating k terms,

-3/(1 - b) = -1/(3 - b)

-3(3 - b) = -1(1 - b)

-9 + 3b = -1 + b

2b = 8

b = 4

k = -1/(3 - 4)

k = 1

p(x) = 1 (x - (-1)) (x - 4)

p(x) = 1 (x + 1) (x - 4)

p(x) = x² - 3x - 4

Problem 6 :

Find the value of a if x − 3 is a factor of f(x) = x³ - 11x + a

Solution :

x - 3 is a factor, then x = 3 is the zero.

f(3) = 3³ - 11(3) + a

0 = 27 - 33 + a

0 = -6 + a

a = 6

Problem 7 :

Find the value of k if f(x) = 3(x² + 3x - 4) - 8(x - k) is divisible by x.

Solution :

It is divisible by x, then x - 0 is a factor.

x = 0

f(0) = 3(0² + 3(0) -  4) - 8(0 - k)

0 = 3(-4) - 8(-k)

0 = -12 + 8k

8k = 12

k = 12/8

k = 3/2

Problem 8 :

If x − 2 is a factor of polynomial 

p(x) = a(x³ - 2x) + b(x² - 5)

which of the following must be true ?

a)  a + b = 0    b) 2a - b = 0    c) 2a + b = 0  d)  4a - b = 0

Solution :

Since x - 2 is a factor, then x = 2 is a zero of the polynomial.

p(2) = a(2³ - 2(2)) + b(2² - 5)

0 = a(8 - 4) + b(4 - 5)

0 = 4a - b

4a - b = 0

So, option d is correct.