PROBLEMS ON REFLECTION OVER Y EQUAL MINUS X

The rule of reflection about y = -x is

(x, y) ==> (-y, -x)

What is preimage ?

Preimage In a transformation, the original figure is called the preimage.

What is image ?

Image In a transformation, the final figure is called the image.

Graph the image of the figure using the transformation given

Problem 1 :

Reflection across y = -x.

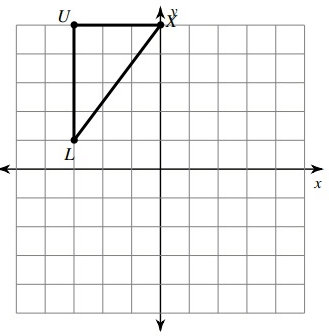
Solution :

By observing the coordinates of the vertices of the triangle given above

X (0, 5), L (-3, 1) and U (-3, 5)

Rule for reflection across y = -x :

(x, y) ==> (-y, -x)

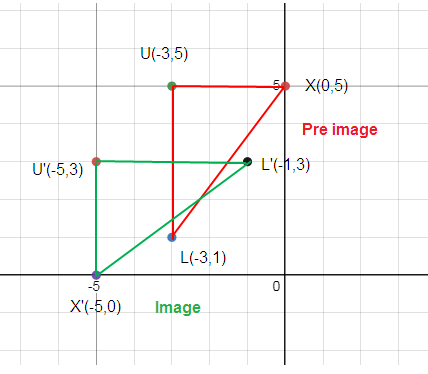
X (0, 5) ==> X’ (-5, 0)

L (-3, 1) ==> L’ (-1, 3)

U (-3, 5) ==> U’ (-5, 3)

Problem 2 :

Reflection across y = -x.

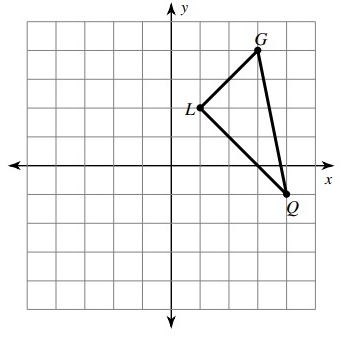
Solution :

By observing the coordinates of the vertices of the triangle given above

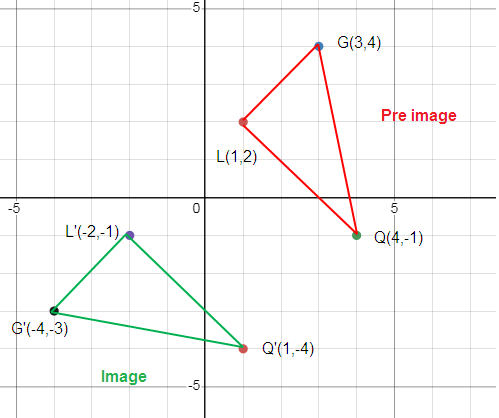
L (1, 2), G (3, 4) and Q (4, -1)

Rule for reflection across y = -x:

(x, y) ==> (-y, -x)

L (1, 2) ==> L’ (-2, -1)

G (3, 4) ==> G’ (-4, -3)

Q (4, -1) ==> Q’ (1, -4)

Problem 3 :

Reflection across the line y = -x

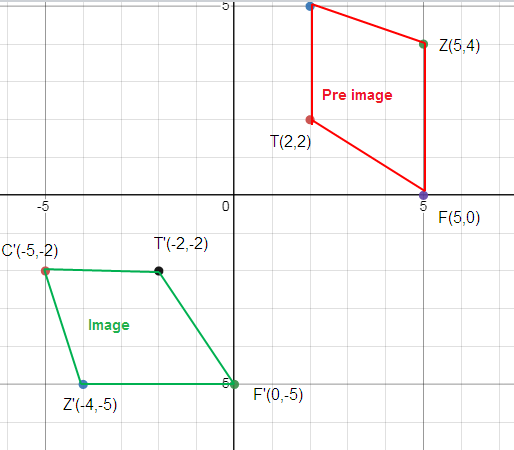
T (2, 2), C (2, 5), Z (5, 4), F (5, 0)

Solution :

Rule for reflection across y = -x:

(x, y) ==> (-y, -x)

T (2, 2) ==> T’ (-2, -2)

C (2, 5) ==> C’ (-5, -2)

Z (5, 4) ==> Z’ (-4, -5)

F (5, 0) ==> F’ (0, -5)

Problem 4 :

Reflection across y = -x.

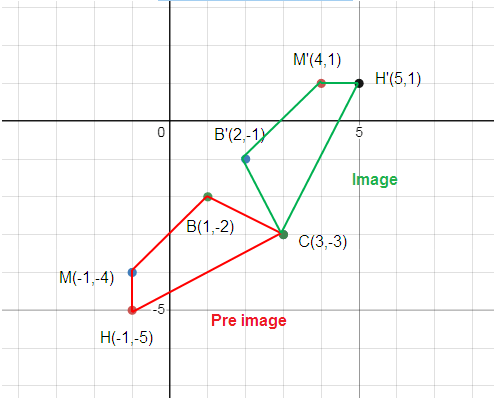
H (-1, -5), M (-1, -4), B (1, -2), C (3, -3)

Solution :

Rule for reflection across y = -x :

(x, y) ==> (-y, -x)

H (-1, -5) ==> H’ (5, 1)

M (-1, -4) ==> M’ (4, 1)

B (1, -2) ==> B’ (2, -1)

C (3, -3) ==> C’ (3, -3)