PROBLEMS ON RATIONAL EXPRESSIONS IN SAT

Problem 1 :

Which of the following is equivalent to

(1/x) / (x + 3)

(a) 1/x(x + 3)  (b)  x/(x + 3)  (c) (x  +3)/3  (d) x(x +3)

Solution :

In the given fraction, we have one fraction in the numerator and integer at the denominator.

= (1/x) / (x + 3)

We can consider the denominator as fraction by considering its denominator is 1.

= (1/x) / (x + 3) / 1

= (1/x) ⋅ [1/(x + 3)]

= 1/x(x + 3)

Problem 2 :

The equation

(kx² + 14x - 20)/(3x - 2) = (5x + 8) - [4/(3x - 2)]

is true for all values of x ≠ 2/3, where k is a constant, what is the value of k ?

(a) 8  (b)  9  (c) 11  (d) 15

Solution :

(kx² + 14x - 20)/(3x - 2) = (5x + 8) - [4/(3x - 2)]

Simplifying the terms that we have in the right side.

(kx² + 14x - 20)/(3x - 2) = [(5x + 8) (3x - 2) - 4] / (3x - 2)

(kx² + 14x - 20)/(3x - 2) = [15x² - 10x + 24x -16 - 4] / (3x - 2)

(kx² + 14x - 20)/(3x - 2) = (15x² + 14x - 20) / (3x - 2)

Comparing the corresponding terms, we get

k = 15

Problem 3 :

The expression (3x² + 4)/(x + 1) is equivalent which of the following ?

(a)  (3x - 3) + 1/(x + 1)    (b) 3x - 3 + 7/(x + 1)

(c)  (3x + 3) + 1/(x + 1)    (b) 3x + 3 + 7/(x + 1)

Solution :

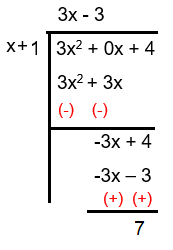
Writing it as mixed number, we get

= (3x - 3) + [7 / (x + 1)]

Problem 4 :

When 3x² + x + 2 is divided by x - 1, the result can be expressed as

(ax + b) + [c/(x - 1)]

where a, b and c are constants. What is the value of

a + b + c ?

Solution :

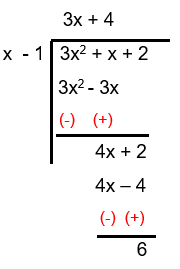
= (3x + 4) + [6/(x-1)]

By comparing the mixed number with (ax + b) + [c/(x - 1)], we get

a = 3, b = 4 and c = 6

a + b + c = 3 + 4 + 6

a + b + c = 13

Problem 5 :

When 2x² - 5x + 3 is divided by 2x + 1, the result can be written as

(x - 3) + [R/(2x+ 1)]

where R is a constant. What is the value of R ?

Solution :

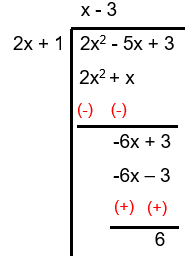
= (x - 3) + [6/(2x +1)]

So, the value of R is 6.

Problem 6 :

What is the one of the possible solution to the equation.

22/(x + 3) - 6/(x - 2) = 1

Solution :

To combine these two rational expressions, we will take the least common multiple, we get

[22(x - 2) - 6(x + 3)] / (x - 2) (x + 3) = 1

(22x - 44 - 6x - 18) / (x - 2) (x + 3) = 1

(16x - 62) / (x² + x - 6) = 1

16x - 62 = (x² + x - 6)

16x - 62 = x² + x - 6

x² + x - 16x - 6 + 62 = 0

x² - 15x + 56 = 0

(x - 7) (x - 8) = 0

Equating each factor to zero, we get

x = 7 and x = 8

Problem 7 :

The expression

(x + 1)/(x + 2) - (x - 2)/(x - 1)

is equivalent to which of the following ?

(a)  -5/(x + 2) (x - 1)    (b)  1/(x + 2) (x - 1)

(c)  3/(x + 2) (x - 1)    (b)  (2x²+3)/(x + 2) (x - 1)

Solution :

To combine the rational expression, let us take the least common multiple.

= [(x + 1)⋅(x - 1)/(x + 2)⋅(x -1)]  - [(x - 2)⋅(x+2)/(x - 1)⋅(x+2)]

= ((x² - 1) - (x² - 4)) / (x - 1)⋅(x + 2)

= (-1 + 4) / (x - 1)(x + 2)

= 3/(x - 1)(x + 2)

Problem 8 :

When 5x + 3 is divided by x + m, where m is a constant, the result can be written as

5 + [ r/(x + m) ]

where r in terms of m ?

Solution :

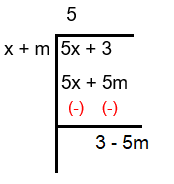
= 5 + (3 - 5m) / (x + m)

Here r = 3 - 5m

Problem 9 :

(x² - x - a) / (x - 2) = (x + 1) - [8/(x - 2)]

In the equation above, what is the value of a ?

Solution :

RHS :

(x + 1) - [8/(x - 2)]

= [(x + 1)(x - 2) - 8]/(x - 2)

= [(x² - x - 2) - 8]/(x - 2)

= (x² - x - 10)/(x - 2)

By comparing the corresponding terms of

x² - x - 10 and x² - x - a

we get a = 10

Problem 10 :

The equation

(24x² + 25x - 47) / (ax - 2) = (-8x - 3) - 53/(ax - 2)

is true for  all values of x ≠ 2/a, where a is constant. What is the value of a ?

Solution :

(24x² + 25x - 47) / (ax - 2) = (-8x - 3) - 53/(ax - 2)

RHS :

= (-8x - 3) - 53/(ax - 2)

= [(-8x - 3) (ax - 2) - 53]/(ax - 2)

= (-8ax² + 16x - 3ax + 6 - 53)/(ax - 2)

= (-8ax² + x(16 - 3a) - 47)/(ax - 2)

Comparing the terms 

(24x² + 25x - 47)  = (-8ax² + x(16 - 3a) - 47)

-8a = 24

a = -24/8

a = -3