PROBLEMS ON PROPORTIONAL AND NON PROPORTIONAL RELAITONSHIPS

Problem 1 :

Determine if each of the following equations represents a proportional or nonproportional relationship.

(i)  q = 2p + (1/2)

(ii)  v = (1/10)u

(iii)  t = 15d

(iv)  m = 0.75d - 2

A linear relationship is a proportional relationship when y/x is constant. Otherwise, the linear relationship is nonproportional.

Solution :

(i)  q = 2p + (1/2)

Here 2p is added by some constant. So, it is non proportional relationship.

(ii)  v = (1/10)u

It is proportional relationship and constant of proportionality is 1/10.

(iii)  t = 15d

It is proportional relationship and constant of proportionality is 15.

(iv)  m = 0.75d - 2

It is not proportional relationship, because 0.75d is subtracted with 2.

From the Table

Problem 2 :

Determine which of the following tables represent proportional relationships.

(i)

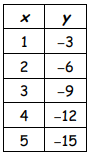Ratio between y to x. k = -3/1 ==> -3 k = -6/2 ==> -3 k = -9/3 ==> -3

Since the constant of proportionality is same. It is proportional relationship.

(ii)

Ratio between y to x. k = -8/(-4) ==> 2 k = -4/(-2) ==> 2 k = 4/2 ==> 2

Since the constant of proportionality is same. It is proportional relationship.

(iii)  

Ratio between y to x. k = -6/(-1) ==> 6 k = -5/0 ==> undefined k = -3/1 ==> -3

Since they are not in the same ratio, it is non proportional relationship.

(iv)

Ratio between y to x. k = -1.5/(-1) ==> 1.5 k = 1.5/1 ==> 1.5 k = 4.5/3 ==> 1.5

Since the constant of proportionality is same. It is proportional relationship.

From the Statement

Problem 3 :

Determine which situation is a proportional relationship and which situation is a nonproportional relationship.

Dylan makes $336 for 32 hours of work, and Angela makes $420 for 42 hours of work.

1) How much do Dylan and Angela each make per hour?

2) Is Dylan’s wage for 25 hours proportional to Amber’s wage for 42 hours? Why or why not?

Solution :

1)

Dylan will make = 336/32 ==> $10.5

Angela will make = 420/42 ==> $10

So, Dylan will make $10.5 and Angela will make $10.

2) Working rate of them are not same, it is not proportional.

Problem 4 :

This year, Andrea celebrated her 12th birthday, and her brother Carlos celebrated his 6th birthday. Andrea noted that she was now twice as old as her brother was. Is the relationship between their ages proportional? Support your answer.

Solution :

Let A be Andrea's age and C be Carlos's age.

A = 2C

So, the relationship between their ages is proportional.

Problem 5 :

Lily is considering buying books on display three different tables. Each table has one of the following signs.

Offer A : Each Book $10

Offer B : Each book 50% off.

Offer C : Each book $8 for club members (one time membership fee : $15).

What will be the total cost if Lily buys 6 books from the table whose sign indicates a nonproportional relationship?

Solution :

Offer C :

Cost of books = 8x + 15

It is non proportional relationship.

From the Graph

Problem 6 :

Complete the tables below and then graph each set of data.

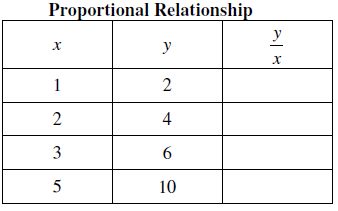
Solution :

It is non proportional relationship.

When x = 1, y = 2, then k = y/x ==> 2/1 ==> 2

When x = 2, y = 4, then k = y/x ==> 4/2 ==> 2

When x = 3, y = 6, then k = y/x ==> 6/3 ==> 2

When x = 5, y = 10, then k = y/x ==> 10/5 ==> 2

By plotting the points (1, 2), (2, 4), (3, 6) and (5, 10) in the graph, we get

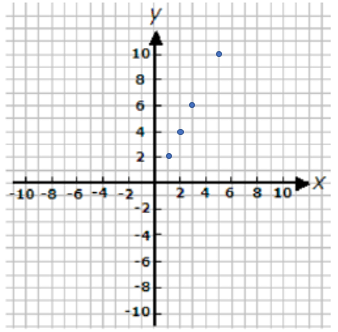
It is a proportional relationship.

Problem 7 :

Determine if each of the following graphs represents a proportional or nonproportional relationship.

(i)

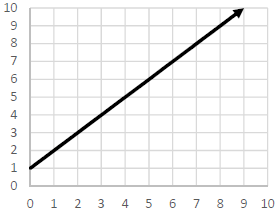
(ii)

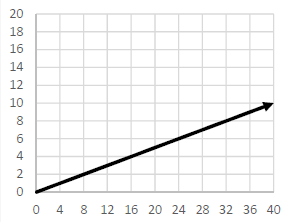
If it is a linear equation it can be written in the form y = mx + b . If it is also proportional, then b = 0 and it can also be written as y = kx .

Solution :

(i)  By considering some of the points (0, 1) (1, 2) (2, 3),......

Finding y/x :

1/0 ==>  undefined

2/1 ==> 2

3/2 ==>  1.5

It is non proportional relationship.

m = (2 - 1)/(1 - 0)

m = 1

y-intercept = 1

So, the required linear equation is y = x + 1.

(ii)  By considering some of the points (0, 0) (8, 2) (16, 4),......

Finding y/x :

2/8 ==>  1/4

4/16 ==>  1/4

It is non proportional relationship.

m = (2 - 0)/(8 - 0)

m = 2/8 ==>  1/4

y-intercept = 0

So, the required equation is y = (1/4)x.