PROBLEMS ON PROPERTIES OF RECTANGLE

Find the values of unknown.

Problem 1 :

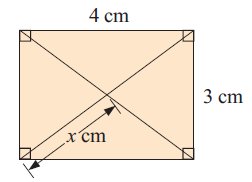
Solution :

Length of the rectangle = 4 cm

Width of the rectangle = 3 cm

Property using :

Diagonals will bisect each other.

AC2 = AB2 + BC2 AC2 = 42 + 32 AC2 = 16 + 9 AC = √25 AC = 5

Half of the diagonal = x ==> 5/2

x = 2.5 cm

Problem 2 :

Find the values of x and y.

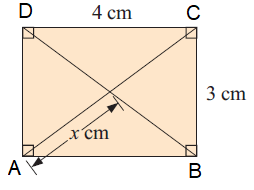
Solution :

Since AB and DC are parallel, DB is transversal.

∠EDC = ∠EBA = 40

Since EB and EA are equal, they will have the equal angle measure.

∠EAB = 40 = x

In triangle EAB,

∠EAB + ∠EBA + ∠AEB = 180

x + x + y = 180

2x + y = 180

2(40) + y = 180

80 + y = 180

Subtracting 80 on both sides.

y = 180 - 80

y = 100

Problem 3 :

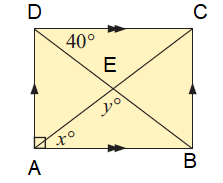
Find the value of x.

Solution :

In a rectangle opposite sides are equal and parallel.

The diagonal is a transversal, so x = 65.

Problem 4 :

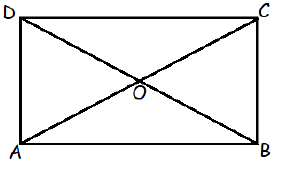
In a given figure, ABCD is a rectangle and its diagonals meet at O. Find x, if OA = 2x + 4 and OD = 3x + 1. Also find BD.

Solution :

OA = OC = 2x + 4

OD = OB = 3x + 1

Property using :

Diagonals are equal and they will bisect each other.

OC = OD

2x + 4 = 3x + 1

2x - 3x = 1 - 4

-x = -3

x = 3

BO = 3(3) + 1 ==> 10

BD = 2BO ==> 2(10) ==> 20

Problem 5 :

The measure of the diagonal of a rectangle is 5 cm. If one of its sides is 3 cm, then find its perimeter.

Solution :

Diagonal of the rectangle = 5 cm.

One of the side = 3 cm.

Since the diagonal will divide the rectangle into two equal right triangles, we can use Pythagorean theorem.

Let x be the missing side of the rectangle.

Diagonal = Hypotenuse

5² = 3² + x²

25 = 9 + x²

Subtracting 9

25 - 9 = x²

x = √16

x = 4

So, the missing side of the rectangle is 4 cm.

Perimeter = 3 + 4 + 5 ==> 12 cm 

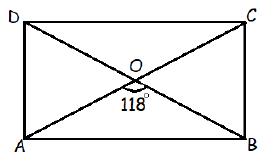
Problem 6 :

ABCD is a rectangle and diagonals intersect at O. If ∠AOB = 118. Find

(i)  ∠ABO    (ii)  ∠ADO      (iii)  ∠OCB

Solution :

(i)  ∠OAB = ∠ABO

In triangle OAB,

∠OAB + ∠ABO + ∠AOB = 180

2∠OBA + 118 = 180

2∠OBA = 180 - 118

2∠OBA = 62

Dividing by 2, we get

∠OBA = 62/2

∠OBA = 31

(ii)  In triangle ADB,

∠ADB + ∠DAB + ∠ABD = 180

∠ADB + 90 + 31 = 180

∠ADB + 121 = 180

∠ADB = 180 - 121

∠ADB = 59

(iii)  ∠DAB = 90

∠DAB = ∠DAO + ∠OAB

90 = ∠DAO + 31

∠DAO = 90 - 31

∠DAO = 59

∠OCB = 59 (Alternate angles)

Problem 7 :

What is the area and length of the diagonal of a rectangle with adjacent side lengths of 24 cm and 7 cm?

Solution :

Adjacent sides of the rectangle is length and width.

length = 24 cm, width = 7 cm

Area of the rectangle = length x width 

= 24 x 7

= 168 cm²

Using Pythagorean theorem :

24² + 7² = Diagonal²

576 + 49 = Diagonal²

Diagonal² = 625

Diagonal = √625

Diagonal = 25

Problem 8 :

The diagonal of a rectangle has a length of 100 cm, and its length is twice its width. Find the area of this rectangle.

Solution :

Diagonal = 100 cm

Let x be the width of the rectangle. Length = 2x

x² + (2x)² = 100²

x² + 4x² = 10000

5x² = 10000

x² = 10000/5

x² = 2000

x = √5 . 5 . 5 . 4 . 4)

x = (5. 4)√5

x = 20√5

Area of rectangle = 2x(x)

= 2x²

= 2(2000)

= 4000 cm²

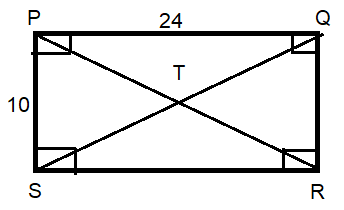
Problem 9 :

Find 

(i)  SQ  (ii)  PR   (iii)  QR   (iv)  SR

Solution :

PQ = 24, PS = 10

Using Pythagorean theorem :

SQ² = SP² + PQ²

SQ² = 10² + 24²

SQ² = 100 + 576

SQ² = 676

SQ = 26

RP = 26 (since the diagonals are equal).

OQ = 10

SR = 24

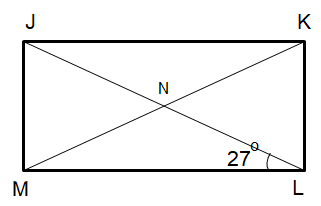
Problem 10 :

Find 

(i)  ∠MJK   (ii)  ∠MJL   (iii)  ∠KML     (iv)  ∠MNL

Solution :

(i)  ∠MJK = 90

(ii)  ∠MJL :

In triangle JML

∠MJL + ∠MLJ + ∠JML = 180

∠MJL + 27 + 90 = 180

∠MJL + 117 = 180

∠MJL = 180 - 117

∠MJL = 63

(iii)  ∠KML :

MN = ML

So, ∠KML = 27

(iv)  ∠MNL

∠NML + ∠NLM + ∠MNL = 180

27 + 27 + ∠MNL = 180

54 + ∠MNL = 180

∠MNL = 180 - 54

∠MNL = 126

Problem 11 :

Find 

(i)  AD   (ii)  BD  (iii)  BC  (iv)  BE

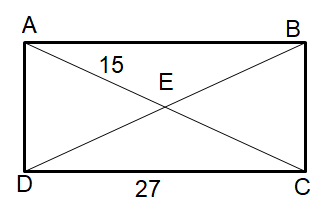
Solution :

AC = 2AE

AC = 2(15) ==>  30

Using Pythagorean theorem :

AD² + DC² = AC²

AD² + 27² = 30²

AD² + 729 = 900

AD² = 900 -729

AD² = 171

AD = √171

(i)  AD = √171  (ii)  BD = 30 

(iii)  BC = √171    (iv)  BE = 15