PROBLEMS ON PROPERTIES OF RECTANGLE INVOLVING DIAGONALS AND ANGLES

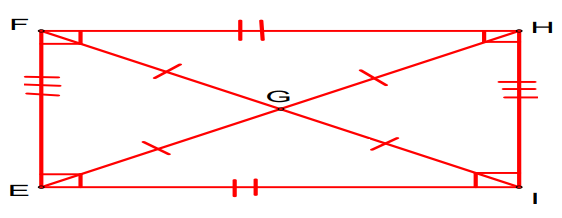
In rectangle, 

• Length of opposite sides will be equal.
• Length of diagonals will be equal.
• Diagonal will bisect each other in the point where it meets each other.
• All corner angles will be right angles.
• Diagonals are not angle bisector of corner angles.

Problem 1 :

PRST is a rectangle, find each angle if m∠1 = 50°

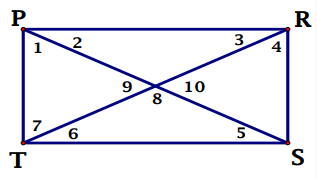
Solution :

Point 1 :

Each corner angle measures will be 90 degree.

∠TPR = ∠1+∠2 = 90

∠1 = 50, ∠2 = ?

50 + ∠2 = 90

∠2 = 90 - 50

∠2 = 40

Point 2 :

Diagonals will bisect each other and diagonals are equal.

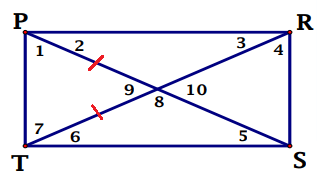
In any triangle, sum of interior angles is 180 degree.

∠1 + ∠7 + ∠9 = 180

∠1 = ∠7 (diagonals are congruent and bisect each other).

∠1 + ∠1 + ∠9 = 180

2∠1 + ∠9 = 180

2(50) + ∠9 = 180

∠9 = 180 - 100

∠9 = 80

∠10 = 80 (vertically opposite angles)

Linear pairs are supplementary

∠9 + ∠8 = 180 

80 + ∠8 = 180 

∠8 = 180 - 80

∠8 = 100 

∠8 = 100 

∠9 = ∠10 (Vertically opposite angles)

∠2 = ∠3 = 40

∠3 + ∠4 = 90

∠4 = 50

∠7 + ∠6 = 90

50 + ∠6 = 90

∠6 = 90 - 50

∠6 = 40

∠5 = 40

∠1 = 50, ∠2 = 40, ∠3 = 40, ∠4 = 50, ∠6 = 40, ∠7 = 50, ∠8 = 100, ∠9 = 80, ∠10 = 80

PRST is a rectangle, find the value of each variable.

Problem 2 :

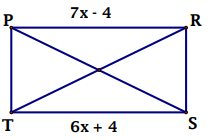
Solution :

In rectangle, the opposite sides will be equal.

PR = TS

7x - 4 = 6x + 4

7x - 6x = 4 + 4

x = 8

Problem 3 :

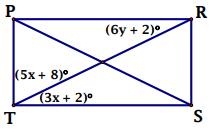
Solution :

In rectangle, each corner angles is 90 degree.

5x + 8 + 3x + 2 = 90

8x + 10 = 90

8x = 90 - 10

8x = 80

x = 80/8

x = 10

Alternate interior angles will be equal. Applying the value of x in 3x + 2, we get

= 3(10) + 2

= 30 + 2

= 32

6y + 2 = 32

6y = 32 - 2

6y = 30

y = 30/6

y = 5

So, the value of x is 10 and value of y is 5.

Problem 4 :

PS = 6x + 3, RT = 7x - 2

Solution :

Here PS and RT are diagonals. In rectangles diagonals will be equal.

PS = RT

6x + 3 = 7x - 2

6x - 7x = -2 - 3

-x = -5

x = 5

Problem 5 :

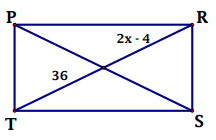
Solution :

Diagonals will bisect each other.

2x - 4 = 36

2x = 36 + 4

2x = 40

x = 40/2

x = 20

Problem 6 :

ABCD is a rectangle, with diagonals that intersect at E. Find the value of each variable

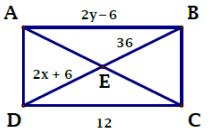
Solution :

In a rectangle, the length of diagonals will be equal.

AC = DB

2x + 6 = 36

2x = 36 - 6

2x = 30

x = 30/2

x = 15

Length of opposite sides will be equal.

2y - 6 = 12

2y = 12 + 6

2y = 18

y = 182/2

y = 9

Problem 7 :

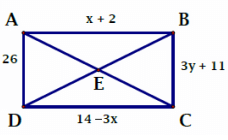
Solution :

In any rectangle, opposite sides will be equal.

Problem 8 :

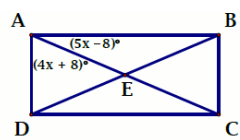
Solution :

In any rectangle, each corner angle is 90 degree.

4x + 8 + 5x - 8 = 90

9x = 90

x = 90/9

x = 10

Problem 9 :

AC = x + 7, DB = 6x - 8

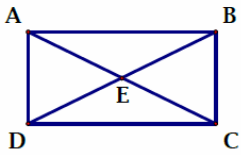
Solution :

In rectangle, length of diagonals will be equal.

AC = BD

x + 7 = 6x - 8

x - 6x = -8 - 7

-5x = -15

x = 15/5

x = 3

Problem 10 :

In the diagram below, ABCD is a rectangle with diagonals AC and BD . If the m∠2 = 58, find the measures of angles 1, 3, and 4.

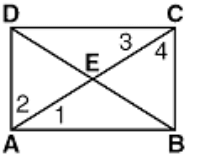
Solution :

m∠2 = 58, 

m∠1 + m∠2 = 90

m∠1 + 58 = 90

m∠1 = 90 - 58

m∠1 = 32

m∠1 = m∠3

m∠2 = m∠4

Problem 11 :

ABCD is a rectangle with diagonals AC and BD. If AC = 6x + 2 and DB = 12x – 10, find the value of x.

Solution :

In rectangle, length of diagonals will be equal.

AC = BD 

6x + 2 = 12x - 10

6x - 12x = -10 - 2

-6x = -12

x = 12/6

x = 2