PROBLEMS ON PARALLEL LINES AND TRANSVERSAL

Find the angle x in each question below. Give reasons for your answer.

Problem 1 :

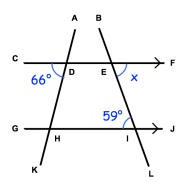
Solution:

CF ∥ GJ

∠FEI = ∠EIH (Alternate interior angle)

x = 59°

Problem 2 :

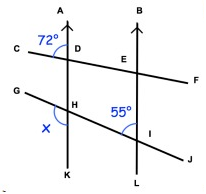
Solution:

AK ∥ BL

∠GIL + ∠GLB = 180°

So, ∠GIL = 180° - ∠GLB

∠GIL = 180° - 55°

∠GIL = 125°

So, x = 125°

Problem 3 :

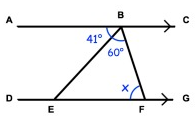
Solution:

AC ∥ DG

∠CBG = ∠BFE (Alternate interior angles)

Angle measures 41, 60 and x are supplementary.

41° + 60° + x = 180°

101° + x = 180°

x = 180° - 101°

x = 79°

Problem 4 :

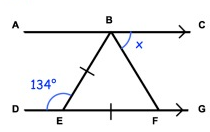
Solution:

∠BEF = 180° - 134° = 46°

∠EBF = ∠EFB = (180 - 46)/2

= 67°

∠DEB = ∠EBC9Alternate interior angles)

134 = 67 + x

x = 134 - 67

x = 67

Problem 5 :

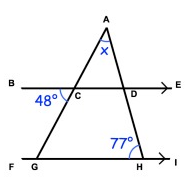
Solution:

∠BCF = 48°

∠AHG = 77°

∠BCG = ∠CGH = 48° (alternate interior angles)

In triangle AGH,

∠AGH + ∠GHA + ∠HAG = 180

48 + 77 + x = 180

125 + x = 180

x = 180 - 125

x = 55°

Problem 6 :

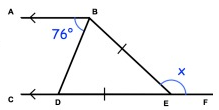
Solution:

AB ∥ CF

∠ABD = ∠BDE (Alternate)

∠BDE = 76°

BE = DE (opposite angle are equal of opposite sides)

x = ∠BDE + ∠DBE (exterior angle is equal to the sum of two opposite interior)

x = 76° + 76°

x = 152°

Problem 7 :

l ∥ m. Find m ∡1 and m∡2

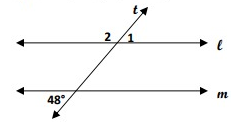
Solution:

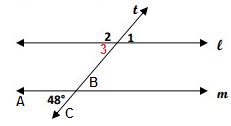
∠3 and ∠ABC are corresponding angle.

l ∥ m

m∠3 = m∠ABC = 48°

∠1 and ∠3 vertically opposite angles.

m∠1 = m∠3 = 48°

m∠2 = 180° - m∠1 

= 180° - 48°

m∠2 = 132°

So, m∠1 = 48° and m∠2 = 132°.

Problem 8 :

a ∥ b. Find x.

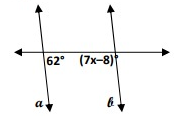
Solution:

a ∥ b

62 and 7x - 8 are cointerior angles.

7x - 8° + 62° = 180°

7x = 188° - 62°

7x = 126°

x = 18°

Problem 9 :

l ∥ m. Find x.

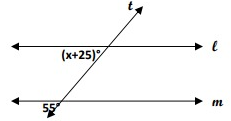
Solution:

l ∥ m

Corresponding angles will be equal. x + 25 and 55 are corresponding angles.

x + 25° = 55°

x = 55° - 25°

x = 30°

Problem 10 :

a ∥ b. Find w.

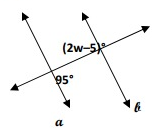
Solution:

a ∥ b

2w-5 and 95 are alternate interior angles and they should be equal.

2w - 5° = 95°

2w = 100°

w = 50°

Problem 11 :

a ∥ b. Find x.

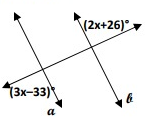
Solution:

a ∥ b

The angles indicated above are alternate exterior angles and they should be equal.

(3x - 33)° = (2x + 26)°

3x - 2x = 26 + 33

x = 59°

Problem 12 :

a ∥ b. Find p.

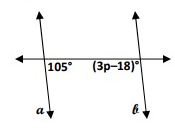
Solution:

a ∥ b

The angles mentioned above are co-interior angles. They add upto 180

105° + (3p - 18)° = 180°

3p + 87° = 180°

3p = 180° - 87°

3p = 93

p = 31°