PROBLEMS ON MODULUS AND PRINCIPAL ARGUMENT OF COMPLEX NUMBER

The length of the line segment, that is OP, is called the modulus of the complex number. The angle from the positive axis to the line segment is called the argument of the complex number, z.

Example :

Find the modulus and argument of a complex number

1 + i

Solution :

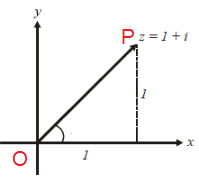
Let z = 1 + i

Finding Modulus :

Sum of squares of real part and imaginary part.

Modulus : OP = |z| = √12 + 12 OP = √2

Argument : θ = tan-1(y/x) θ = tan-1(1/1) θ = tan-1(1) θ = π/4

In the argant plane, angle lies in the 

1st quadrant 2nd quadrant 3rd quadrant 4th quadrant

θ = α θ = π - α θ = -π + α θ = - α

Problem 1 :

The principal argument of 3/(-1 + i) is

Solution :

So, option (3) is correct.

Problem 2 :

The principal argument of (sin 40^º + i cos 40^º)⁵ is

(1)  -110^º    (2)   -70^º   (3)   70^º   (4)   110^º

Solution :

Given, the principal argument of (sin 40^º + i cos 40^º)⁵

= (cos 50^º + i sin 50^º)⁵

= (cos 250^º + i sin 250^º)

250^º lies in III quadrant.

To find the principal argument the rotation must be in a clockwise direction which coincides with 250^º.

θ = -110^º

So, option (1) is correct.

Problem 3 :

If (1 + i) (1 + 2i) (1 + 3i) … (1 + ni) = x + iy, then 2 ⋅ 5 ⋅ 10 … (1 + n²) is

(1)1   (2)   i   (3)   x² + y²    (4)   1 + n²

Solution :

(1 + i) (1 + 2i) (1 + 3i) … (1 + ni) = x + iy

Taking modulus on both sides.

|(1 + i) (1 + 2i) (1 + 3i) … (1 + ni)| = |(x² + y²)|

So, option (3) is correct.

Problem 4 :

If ω ≠ 1 is a cubic root of unity (1 + ω)⁷ = A + Bω, then (A, B) equals

(1)   (1, 0)   (2)   (-1, 1)  (3)   (0,1)   (4)   (1, 1)

Solution :

Given, (1 + ω)⁷ = A + Bω

1 + ω + ω² = 0

1 + ω = -ω²

(1 + ω)⁷ = (-ω²)⁷

= -ω¹⁴

= -ω¹² × ω²

= -(ω³)⁴ × ω²

= -ω²

= 1 + ω

= A + ωB

(A, B) = (1, 1) 

So, option (4) is correct.

Problem 5 :

Solution :

So, option (4) is correct.