PROBLEMS ON MIDPOINT THEOREM OF TRIANGLE

Problem 1 :

D is the Midpoint of AB and E is the Midpoint of BC

If DE = 4x - 9 and AC = 3x + 22, find DE

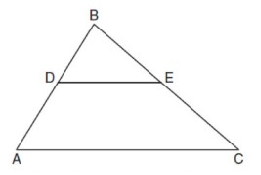
Solution:

Using Midpoint Theorem,

2(DE) = AC

2(4x - 9) = 3x + 22

8x - 18 = 3x + 22

8x - 3x = 22 + 18

5x = 40

x = 8

Finding DE:

DE = 4x - 9

= 4(8) - 9

= 32 - 9

DE = 23

Problem 2 :

D is the Midpoint of AB and E is the Midpoint of BC

If DE = 7x + 1 and AC = 6x + 18, find AC

Solution:

Using Midpoint Theorem,

2(DE) = AC

2(7x + 1) = 6x + 18

14x + 2 = 6x + 18

14x - 6x = 18 + 2

8x = 16

x = 2

Finding AC:

AC = 6x + 18

= 6(2) + 18

= 12 + 18

AC = 30

Problem 3 :

D is the Midpoint of AB and E is the Midpoint of BC

If DE = 2x - 16 and AC = 3x - 3, find DE

Solution:

Using Midpoint Theorem,

2(DE) = AC

2(2x - 16) = 3x - 3

4x - 32 = 3x - 3

4x - 3x = 32 - 3

x = 29

To Find DE:

DE = 2x - 16

= 2(29) - 16

= 58 - 16

DE = 42

Problem 4 :

D is the Midpoint of AB and E is the Midpoint of BC

If DE = 8x - 10 and AC = 10x + 40, find AC

Solution:

Using Midpoint Theorem,

2(DE) = AC

2(8x - 10) = 10x + 40

16x - 20 = 10x + 40

16x - 10x = 40 + 20

6x = 60

x = 10

Finding AC:

AC = 10x + 40

= 10(10) + 40

= 100 + 40

AC = 140

Problem 5 :

If the perimeter of the Large Triangle is 56, find y.

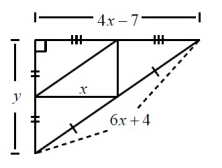
Solution:

P = 4x - 7 + 6x + 4 + y

56 = 10x - 3 + y

59 = 10x - y

y = 59 - 10x ---> (1)

Using Midpoint Theorem,

2(DE) = AC

2x = 4x - 7

2x - 4x = -7

-2x = -7

x = 7/2

By applying x = 7/2 in equation (1)

y = 59 - 10(7/2)

y = 59 - 35

y = 24

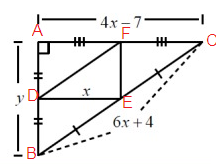
Problem 6 :

If the perimeter of the Large Triangle is 30, find y.

Solution:

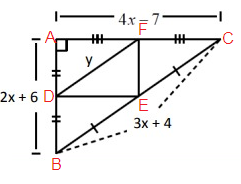
P = 4x - 7 + 3x + 4 + 2x + 6

30 = 9x + 3

9x = 30 - 3

9x = 27

x = 3

Using Midpoint Theorem,

2(DF) = BC

2y = 3x + 4

2y = 3(3) + 4

2y = 9 + 4

2y = 13

y = 6.5

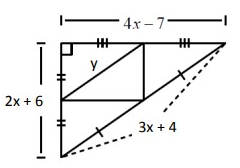
Problem 7 :

If y = 8, find the perimeter of the Smaller Triangle.

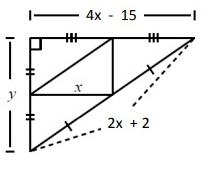
Solution:

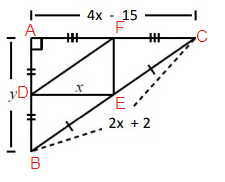
Perimeter of Large Triangle,

P = 4x - 15 + 2x  + 2 + y

Put y = 8,

P = 4x - 15 + 2x + 2 + 8

P = 6x - 5 ---> (1)

Using Midpoint Theorem,

2(DE) = AC

2x = 4x - 15

4x - 2x = 15

2x = 15

x = 15/2

By applying x = 15/2 in (1)

P = 6(15/2) - 5

P = 45 - 5

P = 40

Perimeter of Smaller Triangle,

P = 1/2 (40)

P = 20

Problem 8 :

Find x and y.

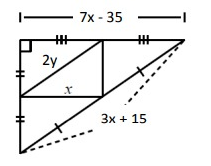
Solution:

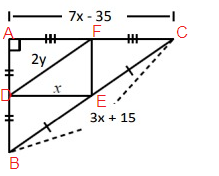
Using Midpoint Theorem,