PROBLEMS ON MIDPOINT FORMULA IN GEOMETRY

Problem 1 :

a)  Given:

PQ = x² + 3, QR = 4 + 2x, PR = 15

Find the value of x.

b) Is Q the midpoint of PR?

Solution:

PQ + QR = PR

x² + 3 + 4 + 2x = 15

x² + 2x + 7 = 15

x² + 2x + 7 - 15 = 0

x² + 2x - 8 = 0

(x + 4) (x - 2) = 0

x + 4 = 0 or x - 2 = 0

x = -4 or x = 2

So, x to be the positive value which is x = 2.

b) Is Q the midpoint of PR?

Solution:

If the distance between PQ and QR are equal, then we decide that Q is the midpoint.

Q is not the midpoint of PR.

Problem 2 :

Find the coordinate of M, the midpoint of GH, for G(8, -6), and H(-14, 12).

Solution:

Let the coordinates of M equal (x, y).

So, the coordinate of M are (-3, 3).

Problem 3 :

Find the coordinates of D if E(-6, 4) is the midpoint of DF and F has coordinates (-5, -3).

Solution:

Let the coordinates of D equal (x, y).

So, the coordinated of D are (-7, 11).

Problem 4 :

M(-3, 2) is the midpoint of RS, and R has coordinates (6, 0). What are the coordinates of S?

Solution:

Let the coordinates of S equal (x, y).

Use the Midpoint Formula,

So, the coordinates of S are (-12, 4).

Problem 5 :

M(7, 1) is the midpoint of WX, and X has coordinates (-1, 5). What are the coordinates of W?

Solution:

Let the coordinates of W equal (x, y).

So, the coordinates of W are (15, -3).

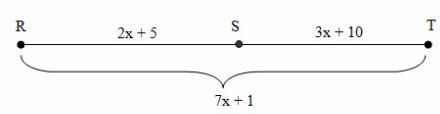
Problem 6 :

What is the measure of ST?

Solution:

RS + ST = RT

2x + 5 + 3x + 10 = 7x + 1

5x + 15 = 7x + 1

5x - 7x + 15 - 1 = 0

-2x + 14 = 0

-2x = -14

x = 7

Measure of ST = 3x + 10

= 3(7) + 10

= 21 + 10

ST = 31

Problem 7 :

Find the coordinates of the midpoint of GH with endpoints G(-4, -7) and H(6, -15).

Solution:

Let the midpoint to be (x, y).

So, the midpoints are (1, -11).

Problem 8 :

M is the midpoint of RS and M has coordinates (-3, 1). R has coordinates (1, -4). Find the coordinates of S.

Solution:

Let the coordinates of S equal (x, y).

Use the Midpoint Formula,

So, the coordinates of S are (-7, 6).

Problem 9 :

Find the length of AM if A has coordinates (-2, 3) and B has coordinates (3, -9), and M is the midpoint of AB.

Solution:

Let the midpoint to be (x, y).

Use the Midpoint Formula,

So, the length of AM is 13/2.