PROLBLEMS ON LINEAR EQUATIONS IN TWO VARIABLES

Problem 1 :

Sketch the graph with equation y = 3x - 6.

Solution:

y = 3x – 6

y-intercept: when x = 0, y = – 6

x-intercept: when y = 0, x = 2

Problem 2 :

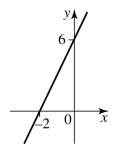
Sketch the graph with equation 2y – 6x – 12 = 0

Solution:

2y - 6x - 12 = 0

y-intercept: when x = 0, y = 6

x-intercept: when y = 0, x = -2

Problem 3 :

Solve the following equations simultaneously:

y = 2x - 1

y = 5x + 2

Solution:

y = 2x - 1

y = 5x + 2

2x - 1 = 5x + 2

-3 = 3x

x = -1 

 y = 2 × (-1) - 1

= -2 - 1

= -3

(x, y) = (-1, -3)

Problem 4 :

What is the point of intersection of the following two lines?

3x + 2y = –10

x + 4y = 5

Solution:

3x + 2y = – 10 ---> (1)

x + 4y = 5 ---> (2)

(1) ×  2 ==> 6x + 4y = –20 ---> (3)

(3) – (2):

5x = –25

x = –5

Substituting x = –5 into equation (1)

3(–5) + 2y = –10

-15 + 2y = -10

2y = 5

y = 2.5

(x, y) = (-5, 2.5)

Problem 5 :

What is the gradient of the line which is perpendicular to the line that connects the two points (–3, 5) and (2, –7)?

Solution:

The two points are(–3, 5) and (2, –7).

The gradient of the perpendicular line is 5/12.

Problem 6 :

What is the equation of the line whose gradient is -3 and which passes through the point (-2, -5)?

Solution:

The equation of the line

y - y₁ = m(x - x₁)

Substitute (x₁, y₁) = (-2, -5) in above equation

y - (-5) = -3[x - (-2)]

y + 5 = -3(x + 2)

y + 5 = -3x - 6

3x + y + 11 = 0

Problem 7 :

What is the gradient of the line that is parallel to the line with equation:

3y - 2x = 6 ?

Solution:

3y - 2x = 6

3y = 2x + 6

The gradient of this line is 2/3. A parallel line will have the same gradient. Therefore the gradient of the line is 2/3.

Problem 8 :

What is the slope of the line with the equation 2x + 3y + 6 = 0 ?

Solution :

2x + 3y + 6 = 0

3y = -2x - 6

y = (-2/3)x - (6/3)

y = (-2/3)x - 2

Slope of the line given is -2/3.

Problem 9 :

Point A (–4, 1) is in the standard (x, y) coordinate plane. What must be the coordinates of point B so that the line x = 2 is the perpendicular bisector of AB ?

Solution :

Let (a, b) be the point B.

Perpendicular bisector means, it will divide the line into two equal parts as well with the angle measure of 90 degree.

Midpoint of AB = (-4 + a)/2, (1 + b)/2

So, the coordinate B is (8, 1).