PROBLEMS ON ISOSCELES TRAPEZOID WITH DIAGONALS

What is Trapezium ?

A trapezium is a convex quadrilateral with exactly one pair of opposite sides parallel to each other. The trapezium is a two-dimensional are called legs. It is also called a trapezoid. Sometimes the parallelogram is also called a trapezoid with two parallel sides.

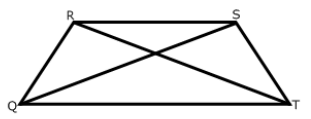
Diagonals are congruent.

Find the length of the diagonal indicated for each trapezoid.

Problem 1 :

DF = 9.1, Find CE

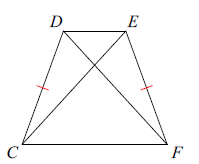
Solution :

CE and DF are diagonals.

DF = 9.1, so CE = 9.1

Solve for x. Each figure is a trapezoid.

Problem 2 :

DF = 6 and CE = 2x - 10

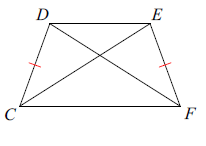
Solution :

DF and CE are diagonals. So, they are equal.

6 = 2x - 10

2x = 6 +10

2x = 16

x = 16/2

x = 8

Problem 3 :

DF = 12 and EG = -2x + 36

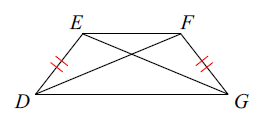
Solution :

DF and EG are diagonals, so they are equal.

DF = EG

12 = -2x + 36

12 - 36 = -2x

-24 = -2x

x = 24/2

x = 12

Find the length of the diagonal indicated for each trapezoid.

Problem 4 :

JL = 2x + 4, KM = 4x - 8. Find JL

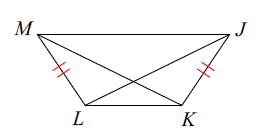
Solution :

JL and KM are diagonals.

JL = MK

2x + 4 = 4x - 8

2x - 4x = -8 - 4

-2x = -12

dividing by -2 on both sides.

x = 12/2

x = 6

Problem 5 :

UW = 3x + 11, TV = 8x - 9 and Find UW

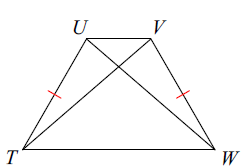
Solution :

UW and TV are diagonals.

UW = TV

3x + 11 = 8x - 9

Subtracting 8x and 11, we get

3x - 8x = -9 - 11

-5x = -20

x = 20/5

x = 4

Problem 6 :

The bases of an isosceles trapezoid ABCD measure 10 cm and 20 cm. The height (altitude) is 12 cm. How long are the legs AB and CD?

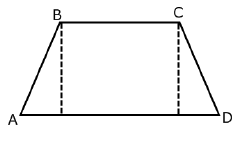
Solution :

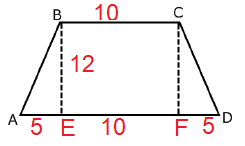
In triangle ABE,

AB² = AE² + BE²

AB² = 5² + 12²

AB² = 25 + 144

AB² = 169

AB = 13

Since is it isosceles trapezoid, CD is 13.

Problem 7 :

In isosceles trapezoid KIME, <K and <E are the base angles. If IK = 11 and ME = 3x - 1, what is the value of x?

Solution :

In KIME, KI and ME are non parallel sides.

IM and KE are parallel sides.

Non parallel sides will be equal in length.

IK = ME

11 = 3x - 1

Add 1 on both sides.

11 + 1 = 3x

3x = 12

x = 12/3

x = 4

Problem 8 :

𝐴𝐵𝐶𝐷 is an isosceles trapezoid with bases 𝐴𝐵 and 𝐷𝐶. If 𝐴𝐷 = 3x+4 and 𝐵𝐶 = x+12. Find the value of x and the length of 𝐴𝐷.

Solution :

AD = BC

3x + 4 = x + 12

3x - x = 12 - 4

2x = 8

x = 8/2

x = 4