PROBLEMS ON INTERIOR AND EXTERIOR ANGLES OF POLYGON

Problem 1 :

The number of sides of a regular polygon where each exterior angle has a measure of 45^º is ……

a)  8        b) 10       c) 4     d) 6

Solution :

Sum of the exterior angles of a regular polygon = 360 ^º

Exterior angle has a measure = 45^º

Number of sides of a regular polygon = 360/45

= 8

Number of sides of a regular polygon is 8 sides.

Hence, option a. is correct.

Problem 2 :

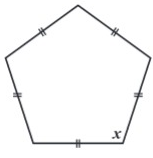
a)  60^º      b) 140^º      c) 150^º     d) 108^º

Solution :

A regular pentagon has all its five sides equal and all five angles are also equal.

S = [(n – 2) × 180^º]/n

= [(5 – 2) × 180^º]/5

= (3 × 180^º)/5

= 540^º/5

= 108^º

Hence, option d. is correct.

Problem 3 :

If two adjacent angles of a parallelogram are in the ratio 2 : 3, then the measure of angles are 

(a) 72^º, 108^º     (b) 36^º, 54^º     (c) 80^º, 120^º    (d) 96^º, 144^º

Solution :

Let the two adjacent angles of a parallelogram are in the ratio be 2x and 3x.

So, 2x + 3x = 180^º

[Interior angles on the same side of transversal].

5x = 180^º

Dividing 5 on both sides.

5x/5 = 180^º/5

x = 36^º

Therefore the measure of angles are, 

2 × 36^º = 72^º

2 × 36^º = 108^º

Hence, option a. is correct.

Problem 4 :

If PQRS is a parallelogram, then ∠P - ∠R is equal to

a) 60^º     b) 90^º    c) 80^º    d) 0^º

Solution :

Opposite angles are equal to each other in parallelogram.

Given, ∠P - ∠R

∠P = ∠R

∠R - ∠R = 0^º

Hence, option d. is correct.

Problem 5 :

The sum of adjacent angles of a parallelogram is

a) 180^º     b) 120^º  c) 360^º  d) 90^º

Solution :

The sum of adjacent angles of a parallelogram is 180^º. Because both angles are co – interior angles.

Hence, option a. is correct.

Problem 6 :

The number of sides of a regular polygon whose each interior angle is of 135^º is ……

a) 6       b) 7      c) 8        d) 9

Solution :

Sum of colinear interior and exterior angle is 180^º.

Interior angle + exterior angle = 180^º

135^º + exterior angle = 180^º

Exterior angle = 180^º - 135^º

Exterior angle = 45^º

Number of sides of a regular polygon = 360^º/Exterior angle

= 360^º/45^º

= 8

So, the number of sides of a regular polygon is 8.

Hence, option c. is correct.