PROBLEMS ON INTERIOR AND EXTERIOR ANGLES OF A POLYGON

Find the indicated angle measures, x.

Problem 1 :

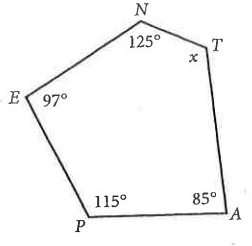
Solution :

The sum of the exterior angle of polygon = (n - 2) × 180°

= (5 - 2) × 180°

= 3 × 180°

= 540°

∠P + ∠A + ∠E + ∠N + ∠T = 540°

115° + 85° + 97° + 125° + x° = 540°

422° + x° = 540°

x° = 540 - 422

x° = 118

Problem 2 :

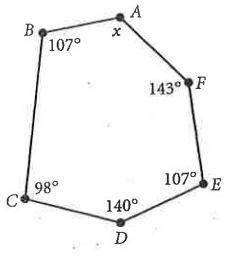
Solution :

The sum of the exterior angle of polygon = (n - 2) × 180°

= (6 - 2) × 180°

= 4 × 180°

= 720°

∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 720°

x° + 107° + 98° + 140° + 107° + 143° = 720°

595° + x° = 720°

x° = 720 - 595

x° = 125

Problem 3 :

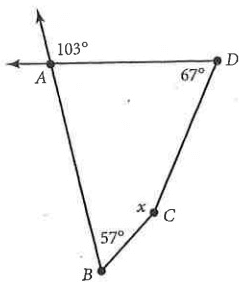
Solution :

The sum of the exterior angle of polygon = (n - 2) × 180°

= (4 - 2) × 180°

= 2 × 180°

= 360°

∠BAD = 180° - 103°

∠BAD = 77°

∠BAD + ∠D + ∠B + ∠C = 360°

77° + 67° + 57° + x° = 360°

201° + x = 360°

x° = 360 - 201

x° = 159 

Problem 4 :

An exterior angle and the interior angle of a regular polygon are in the ratio 2:7. Find the number of sides of the polygon.

Solution :

Let x be the interior angle, then 180-x be the exterior angle.

(180-x) : x = 2 : 7

(180-x)/x = 2 / 7

2x = 7(180-x)

2x = 1260 - 7x

2x + 7x = 1260

9x = 1260

x = 1260/9

x = 40

Exterior angle is 40 degree. Interior angle = 140

Hence, the number of sides in the polygon is 9.

Problem 5 :

Find the number of sides of a regular polygon whose each exterior angle measures 60°.

Solution :

Sum of all exterior angles = 360°

n × 60 = 360

n = 360/60

n = 6

Hence, the number of sides in the polygon is 6. 

Find x in :

Problem 6 :

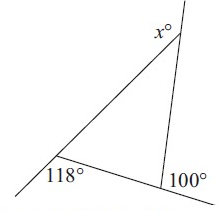
Solution :

The sum of the exterior angle of any polygon is 360°.

118° + 100° + x° = 360°

218° + x° = 360°

x° = 360 - 218

x° = 142

Problem 7 :

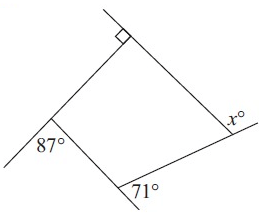
Solution :

The sum of the exterior angle of any polygon is 360°.

87° + 71° + 90° + x° = 360°

248° + x° = 360°

x° = 360 - 248

x° = 112

Problem 8 :

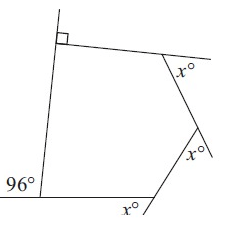
Solution :

The sum of the exterior angle of any polygon is 360°.

96° + 90° + x° + x° + x° = 360°

186° + 3x° = 360°

3x° = 360° - 186°

3x° = 174

x° = 174/3

x° = 58