PROBLEMS ON GEOMETRY PROPERTIES OF PARALLELOGRAM WITH DIAGONALS

Properties of Parallelogram

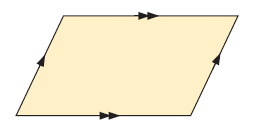
In parallelogram, opposite sides are parallel and equal.

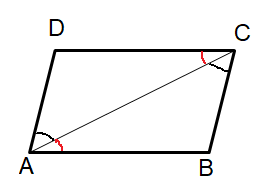
Here diagonal is like a transversal for parallel lines. Then alternate interior angles are equal.

That is, 

∠DAC = ∠ACB, ∠DCA = ∠CAB 

Since the opposite sides are parallel, we observe the same side interior angles.

∠DAB + ∠ADC = 180

∠DCB + ∠CBA = 180

Conclusion :

• Opposite sides are equal
• Opposite angles are equal
• Sum of consecutive interior angles will be 180 degree.
• Diagonals will bisect each other.

Problem 1 :

Find angle measure ∠YWX.

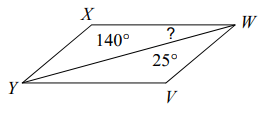
Solution :

Opposite angles are equal.

∠X = 140

∠V = 140

∠V + ∠WYV + ∠VWY = 180

140 + ∠WYV + 25 = 180 

165 + ∠WYV = 180 

∠WYV = 180 - 165

∠WYV = 15

∠YWX = 15 (alternate interior angles).

Problem 2 :

Find ∠KLJ.

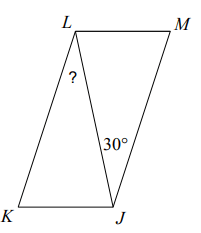
Solution :

In parallelogram, diagonal is a transversal of parallel lines.

∠KLJ = ∠LJM

Alternate interior angles.

∠KLJ = 30

Problem 3 :

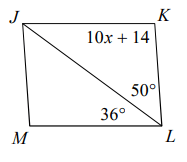
Solution :

∠MLJ = ∠LJK

In the triangle JLK,

∠JLK + ∠LKJ + ∠KJL = 180

50 + 10x + 14 + 36 = 180

10x + 14 + 86 = 180

10x + 100 = 180

10x = 180 - 100

10x = 80

x = 80/10

x = 8

Problem 4 :

FH = 14, QH = 2x - 13

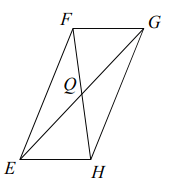
Solution :

In a parallelogram, the diagonals will be equal. Diagonals will bisect each other.

FH = 2QH

14 = 2(2x - 13)

14/2 = 2x - 13

7 = 2x - 13

2x = 7 + 13

2x = 20

x = 20/2

x = 10

Problem 5 :

CJ = 5 + 3x, JE = 2x + 11 and find CJ.

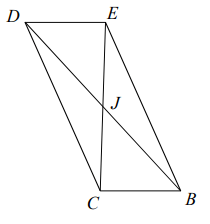
Solution :

CJ = JE

5 + 3x = 2x + 11

5 - 11 = 2x - 3x

-6 = -x

x = 6

Applying the value of x in CJ = 5 + 3x

CJ = 5 + 3(6)

= 5 + 18

CJ = 23

Problem 6 :

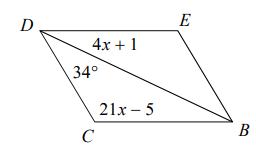
Solution :

∠EDB = ∠DBC

∠DBC = 4x + 1

∠DCB + ∠CBD + ∠CDB = 180

21x - 5 + 4x + 1 + 34 = 180

21x + 4x - 4 + 34 = 180

25x + 30 = 180

25x = 180 - 30

25x = 150

x = 150/25

x = 6