PROBLEMS ON EQUILATERAL TRIANGLE

Problem 1 :

Find the length of each side of an equilateral triangle having an area of 9√3 cm².

Solution:

Given, the area of equilateral triangle is 9√3 cm².

The area of equilateral triangle = (√3/4) a²

(√3/4) a² = 9√3

a² = 9 × 4

a² = 36

a = 6 cm

Hence, the side of the triangle is 6 cm.

Problem 2 :

If the area of an equilateral triangle is 16√3 cm², then find the perimeter of the triangle.

Solution:

Given, area of an equilateral triangle = 16√3 cm²

Area of an equilateral triangle = (√3/4) a² 

(√3/4) a² = 16√3

a² = 64

a = 8 cm

Perimeter of an equilateral triangle = 3a

= 3 × 8

= 24 cm

Hence, the perimeter of an equilateral triangle is 24  cm. 

Problem 3 :

One side of an equilateral triangle has length (4x+7). Another side has length (3x+8). Find the perimeter of the triangle.

Solution :

Sides of the triangles are 4x + 7 and 3x + 8

Since it is equilateral triangle, they will have equal measures.

4x + 7 = 3x + 8

4x - 3x = 8 - 7

x = 1

Perimeter of the equilateral triangle = 3(4x + 7)

= 3 (4(1) + 7)

= 3 (4 + 7)

= 3(11)

= 33 cm

Problem 4 :

The perimeter of an equilateral triangle is equal to the perimeter of a rectangle with a length of 5 cm and a width of 4 cm. Find the length of one side of the triangle.

Solution :

Perimeter of equilateral triangle = perimeter of rectangle

3a = 2(length + width)

3a = 2(5 + 4)

3a = 2(9)

a = 18/3

a = 6

So, side length of the triangle is 6 cm.

Problem 5 :

The diagram shows an equilateral triangle. Find the length of its sides.

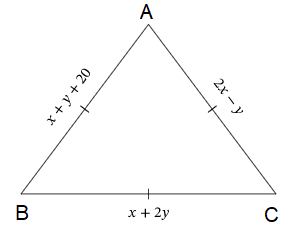
Solution :

AB = AC

x + y + 20 = 2x - y

x - 2x + y + y = -20

-x + 2y = -20 -----(1)

AB = BC

x + y + 20 = x + 2y

x - x + y - 2y = -20

-y = -20

y = 20

Applying the value of y in (1), we get

-x + 2(20) = -20

-x + 40 = -20

-x = -20 - 40

-x = -60

x = 60

Problem 7 :

Calculate the length of one of the sides of an equilateral triangle which has a perimeter of 93 m.

Solution :

Perimeter of the equilateral triangle = 93 m

3a = 93

a = 93/3

a = 31 m

So, side length of the equilateral triangle is 31 m.

Problem 8 :

What is the value of x, if triangle ABC is equilateral triangle.

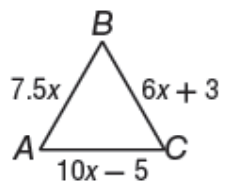
Solution :

Since it is equilateral triangle, then AB = BC = CA

7.5x = 6x + 3

7.5x - 6x = 3

1.5x = 3

x = 3/1.5

x = 2