PROBLEMS ON DOMAIN AND RANGE OF EXPONENTIAL FUNCTIONS
Problem 1 :
What is the domain of the exponential function
f(x) = 14(0.8)x ?
Solution :
f(x) = 14(0.8)x
Domain for exponential function will be all real number, so domain is (-∞, ∞).
Problem 2 :
What is the range of exponential function y = 120 (7x) ?
Solution :
Finding horizontal asymptote for the exponential function, it is easier to fix the range.
The function which is in the form y = abx - h + k
Here y = k is the horizontal asymptote.
Here the horizontal asymptote is y = 0, then range is y > 0
Problem 3 :
The graph of y = (2/3)x is shown below. What is the range of the function y ?
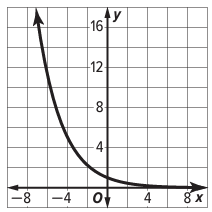
Solution :
From the graph, the horizontal asymptote is y = 0. Then the range is y > 0.
Problem 4 :
What is the domain of f(x) = 6(1.8)x?
Solution :
Domain of the function is all real values.
Problem 5 :
The graph of the exponential function y = -400 (5)x is shown below.
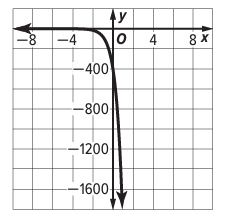
What is the range of the function ?
Solution :
From the graph, there is a reflection across x-axis, it is decreasing function.
So, the range is y < 0.
Problem 6 :
The table below shows points that belongs to the function.
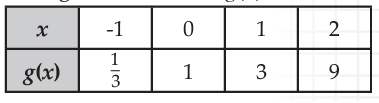
Solution :
Exponential function will be in the form y = abx -------(1)
Applying the point (0, 1) in the function, we get
1 = ab0
1 = a(1)
a = 1
By applying the value of a in (1), we get
y = 1(b)x
By applying the point (1, 3), we get
3 = 1(b)1
b = 3
So, the required function is y = 3x .
- Domain is all real values.
- Range is y > 0.
Problem 7 :
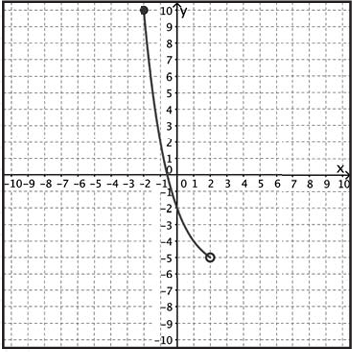
Solution :
Domain is x < 2.
Horizontal asymptote is y = -5, so the range is y > -5.
Problem 8 :
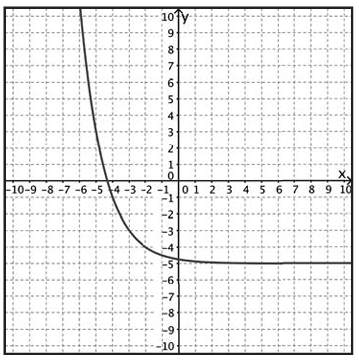
Solution :
Domain is all real values.
Horizontal asymptote is y = -5, so the range is y > -5.
Problem 9 :
The volume V, the air remaining in an inflated balloon can be modeled by the function
V = 1000 (0.85)x
where x represents the number of days that have passed since inflating the balloon. What is the reasonable domain for the situation.
Solution :
V = 1000 (0.85)x
Since it is exponential function, it is defined for every real numbers.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling